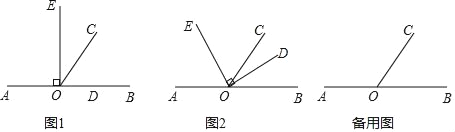
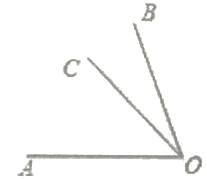
【题目】如图所示,在直线AB上的一点O,以O为端点依次作射线OE,OC,OD,使∠EOD=90°,∠COB=60°
(1)如图1当∠EOD的一边OD在射线OB上时,求∠COE的度数;
(2)如图2当∠EOD绕着点O逆时针旋转到OC平分∠BOE时,求∠COD的度数;
(3)当∠EOD绕着点O逆时针旋转,且O°<∠AOE<90°(但≠60°)时,试猜想∠AOE与∠COD有怎样的数量关系,并说明理由.
参考答案:
【答案】(1)30;(2)30°;(3)当60°<∠AOE<90°时,∠AOE﹣∠COD=30°;当0<∠AOE<60°时,∠AOE+∠COD=30°;
【解析】
(1)根据∠COE=∠EOB-∠BOC计算即可;
(2)根据∠COD=∠EOD-∠EOC,只要求出∠EOC即可;
(3)当60°<∠AOE<90°时,∠AOE-∠COD=30°;当0<∠AOE<60°时,∠AOE+∠COD=30°.
(1)∵∠COE=∠EOB﹣∠BOC,∠EOD=90°,∠COB=60°
∴∠COE=90°﹣60°=30°,
(2)∵OC 平分∠BOE,
∴∠BOC=∠COE=60°,
∴∠COD=∠EOD﹣∠EOC=90°﹣60°=30°;
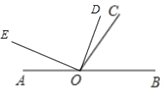
(3)①如图2中,当60°<∠AOE<90°时,
∵∠EOD=90°,
∴∠AOE+∠DOB=90°,
∴∠AOE+(60°﹣∠COD)=90°,
∴∠AOE﹣∠COD=30°
②如图3中,当0<∠AOE<60°时,∵∠AOC=180°﹣∠BOC=120°,∠EOD=90°,
∴∠AOE+∠COD=30°;
综上所述,当60°<∠AOE<90°时,∠AOE﹣∠COD=30°;
当0<∠AOE<60°时,∠AOE+∠COD=30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解全校学生上学期参加“生涯规划”社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
参加社区活动次数的频数、频率
活动次数x
频数
频率
0<x≤3
10
0.20
3<x≤6
a
0.24
6<x≤9
16
0.32
9<x≤12
6
0.12
12<x≤15
b
m
15<x≤18
2
n
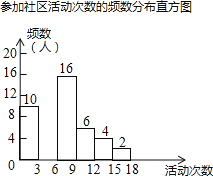
根据以上图表信息,解答下列问题:
(1)表中a= , b= , m= , n= .
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将一点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这一点的“互换点”,如(﹣3,5)与(5,﹣3)是一对“互换点”.
(1)任意一对“互换点”能否都在一个反比例函数的图象上?为什么?
(2)M、N是一对“互换点”,若点M的坐标为(m,n),求直线MN的表达式(用含m、n的代数式表示);
(3)在抛物线y=x2+bx+c的图象上有一对“互换点”A、B,其中点A在反比例函数y=﹣ 的图象上,直线AB经过点P(
的图象上,直线AB经过点P(  ,
,  ),求此抛物线的表达式.
),求此抛物线的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,对角线AC与BD相交于O,AB=6cm, ∠BAO=30°,点F为AB的中点.
(1)求OF的长度;
(2)求AC的长.

-
科目: 来源: 题型:
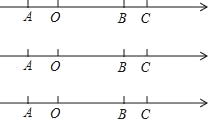
查看答案和解析>>【题目】如图数轴上A、B、C三点对应的数分别是a、b、7,满足OA=3,BC=1,P为数轴上一动点,点P从A出发,沿数轴正方向以每秒1.5个单位长度的速度匀速运动,点Q从点C出发在射线CA上向点A匀速运动,且P、Q两点同时出发.
(1)求a、b的值
(2)当P运动到线段OB的中点时,点Q运动的位置恰好是线段AB靠近点B的三等分点,求点Q的运动速度
(3)当P、Q两点间的距离是6个单位长度时,求OP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表
售价x(元)
15
20
25
日销售量y(件)
25
20
15
若日销售量y是销售价x的一次函数.
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)求销售价定为30元时,每日的销售利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】题目:在同一平面上,若∠AOB=75°,∠BOC=15°,求∠AOC的度数.
下面是七(2)班马小虎同学的解题过程:
解:根据题意画出图形,如图所示,
∵∠AOC=∠AOB-∠BOC=75°-75°=60°
∴∠AOC=60°
若你是老师,会判马小虎满分吗?若会,说明理由;若不会,请指出错误之处,并给出你认为正确的解法.
相关试题

