搜索
【题目】解方程
（1）（x﹣5）2=16（直接开平方法） （2）x2﹣4x+1=0（配方法）
（3）x2+3x﹣4=0（公式法） （4）x2+5x﹣3=0（配方法）
参考答案：
【答案】（1）x1=9，x2=1；（2）x1=2+
，x2=2﹣
；（3）x1=1，x2=﹣4；（4）x1=
，x2=
．
【解析】试题分析：（1）按要求利用直接开平方法进行求解即可；
（2）按要求利用配方法根据配方法的步骤进行求解即可；
（3）按要求利用公式法进行求解即可；
（4）按要求利用配方法根据配方法的步骤进行求解即可.
试题解析：（1）（x﹣5）2=16，
x-5=±4，
x-5=4或x-5=-4，
∴x1=9，x2=1；
（2）x2﹣4x+1=0，
x2﹣4x=-1，
x2﹣4x+4=-1+4，
（x-2）2=3，
x-2=±
，
∴x1=2+
，x2=2﹣
；
（3）x2+3x﹣4=0，
a=1，b=3，c=-4，
b2-4ac=32-4×1×(-4)=25>0，
，
∴x1=1，x2=﹣4；
（4）x2+5x﹣3=0，
x2+5x=3，
x2+5x+
=3+
，
，
，
∴x1=
，x2=
．
-
科目： 来源： 题型：
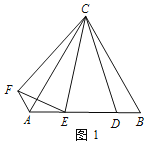
查看答案和解析>>【题目】【操作发现】如图 1，△ABC 为等边三角形，点 D 为 AB 边上的一点，∠DCE=30°，将线段 CD 绕点 C 顺时针旋转 60°得到线段 CF，连接 AF、EF. 请直接 写出下列结果：
① ∠EAF的度数为__________；
② DE与EF之间的数量关系为__________；
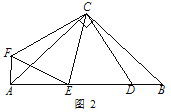
【类比探究】如图 2，△ABC 为等腰直角三角形，∠ACB=90°，点 D 为 AB 边上的一点∠DCE=45°，将线段 CD 绕点 C 顺时针旋转 90°得到线段 CF，连接 AF、EF.
①则∠EAF的度数为__________；
② 线段 AE，ED，DB 之间有什么数量关系？请说明理由；
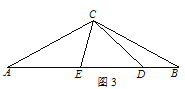
【实际应用】如图 3，△ABC 是一个三角形的余料.小张同学量得∠ACB=120°，AC=BC， 他在边 BC 上取了 D、E 两点，并量得∠BCD=15°、∠DCE=60°，这样 CD、CE 将△
ABC 分成三个小三角形，请求△BCD、△DCE、△ACE 这三个三角形的面积之比.
-
科目： 来源： 题型：
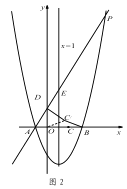
查看答案和解析>>【题目】如图1，对称轴为直线x=1的抛物线y=
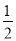x2+bx+c，与x轴交于A、B两点（点A在点B的左侧），且点A坐标为(-1，0).又P是抛物线上位于第一象限的点，直线AP与y轴交于点D，与抛物线对称轴交于点E，点C与坐标原点O关于该对称轴成轴对称.（1）求点 B 的坐标和抛物线的表达式；
（2）当 AE：EP=1：4 时，求点 E 的坐标；
（3）如图 2，在（2）的条件下，将线段 OC 绕点 O 逆时针旋转得到 OC ′，旋转角为 α(0°＜α＜90°)，连接 C ′D、C′B，求 C ′B+
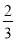C′D 的最小值．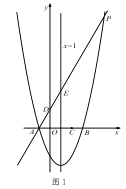
-
科目： 来源： 题型：
查看答案和解析>>【题目】把下列各数的序号填在相应的横线上：
①﹣5.32，②3，③﹣1
，④7%，⑤0，⑥﹣5，⑦0.6，⑧+2019（1）整数有：_____
（2）分数有：_____
（3）负数有：_____
（4）正数有：_____
（5）非负数有：_____
（6）有理数有：_____
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，用同样规格黑白两色的正方形瓷砖铺设长方形地面，请观察下列图形，并解答有关问题：
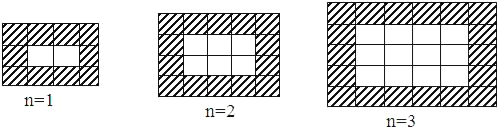
（1）在第n个图中，第一横行共 块瓷砖，第一竖列共有 块瓷砖；（均用含n的代数式表示）铺设地面所用瓷砖的总块数为 （用含n的代数式表示，n表示第n个图形）
（2）上述铺设方案，铺一块这样的长方形地面共用了506块瓷砖，求此时n的值；
（3）黑瓷砖每块4元，白瓷砖每块3元，在问题（2）中，共需要花多少钱购买瓷砖？
（4）是否存在黑瓷砖与白瓷砖块数相等的情形？请通过计算加以说明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知反比例函数
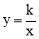（k为常数，k≠0）的图象经过点A（2，3）．（1）求这个函数的解析式；
（2）判断点B（－1，6），C（3，2）是否在这个函数的图象上，并说明理由；
（3）当－3＜x＜－1时，求y的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察图形，解答问题：
（1）按下表已填写的形式填写表中的空格：
图①
图②
图③
三个角上三个数的积
1×（－1）×2＝－2
（－3）×（－4）×（－5）＝－60
三个角上三个数的和
1＋（－1）＋2＝2
（－3）＋（－4）＋（－5）＝－12
积与和的商
（－2）÷2＝－1
（2）请用你发现的规律求出图④中的数x和图⑤中的数y．
相关试题
