搜索
【题目】如图，在等腰三角形
中，
，
为
边上中点，过点作
，交
于
，交
于
，若
，则的长为_________．
参考答案：
【答案】6
【解析】
连接BD，利用ASA证出△EDB≌△FDC，从而证出S△EDB=S△FDC，从而求出S△DBC，然后根据三角形的面积即可求出CD，从而求出AC，最后利用勾股定理即可求出结论．
解：连接BD
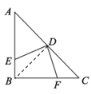
∵在等腰三角形
中，
，
为
边上中点，
∴AB=BC，BD=CD=AD，∠BDC=90°，∠EBD=
，∠C=45°
∵
∴∠EDF=∠BDC=90°，∠EBD=∠C=45°
∴∠EDB=∠FDC
在△EDB和△FDC中
∴△EDB≌△FDC
∴S△EDB=S△FDC
∴S△DBC= S△FDC＋S△BDF= S△EDB＋S△BDF=
∴
∴CD2=18
∴CD=
∴AC=2CD=
∴AB2＋BC2=AC2
∴2AB2=（）2
故答案为：6．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A，B的坐标分别为(－1，0)，(3，0)，现同时将点A，B分别向上平移2个单位长度，再向右平移1个单位长度，得到A，B的对应点C，D，连接AC，BD，CD.
(1)直接写出点C，D的坐标，求出四边形ABDC的面积；
(2)在x轴上是否存在一点F，使得三角形DFC的面积是三角形DFB面积的2倍，若存在，请求出点F的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了解学生对校园网站五个栏目的喜爱情况（规定每名学生只能选一个最喜爱的）.学校随机抽取了部分学生进行调查，将调查结果整理后绘制成如下两幅不完整的统计图，请结合图中提供的信息解答下列问题：
（1）本次被调查的学生有_____人，扇形统计图中m =_____；
（2） 将条形统计图补充完整；
（3）若该校有1800名学生，估计全校最喜爱“校长信箱”栏目的学生有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】己知二次函数
. 
(1)写出其顶点坐标为 ，对称轴为 ;
(2)在右边平面直角坐标系内画出该函数图像;
(3)根据图像写出满足
的
的取值范围 . -
科目： 来源： 题型：
查看答案和解析>>【题目】标有－3，－2，4的三张不透明的卡片，除正面写有不同的数字外，其余的值都相同，将这三张卡片背面朝上洗匀后，第一次从中随机抽取一张，并把这张卡片标有的数字记为一次函数解析式y＝kx＋b的k值，第二次从余下的两张卡片中再抽取一张，上面标有的数字记为一次函数解析式的b值．
(1)写出k为负数的概率；
(2)求一次函数y＝kx＋b的图象不经过第一象限的概率．（用树状图或列举法求解）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点
的坐标为
，作
轴，
轴，垂足分别为
，
，点
为线段
的中点，点
从点出发，在线段
、
上沿
运动，当
时，点的坐标为________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB⊥BC，AD⊥DC，∠BAD=100°，在BC、CD上分别找一点M、N，当△AMN的周长最小时，∠AMN+∠ANM的度数是_____．
相关试题
