【题目】一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x小时,两车之间的距离为y千米,图中的折线表示y与x之间的函数关系.当两车之间的距离首次为300千米时,经过_____小时后,它们之间的距离再次为300千米.

参考答案:
【答案】3
【解析】根据题意和折线图,可知:
(480﹣440)÷0.5=80km/h,
440÷(2.7﹣0.5)﹣80=120km/h,
所以,慢车速度为80km/h,
快车速度为120km/h;
由题意,可知两车行驶的过程中有2次两车之间的距离为300km.
即相遇前:(80+120)×(x﹣0.5)=440﹣300,
解得x=1.2(h),
相遇后:(80+120)×(x﹣2. 7)=300,
解得x=4.2(h),
4.2﹣1.2=3(h)
所以当两车之间的距离首次为300千米时,经过3小时后,它们之间的距离再次为300千米
故答案为:3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】防洪大堤的横截面如图所示,已知AE∥BC,背水坡AB的坡度
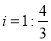 ,且AB=20米.身高1.7米的小明竖直站立于A点,眼睛在M点处测得竖立的高压电线杆顶端D点的仰角为24°,已知地面CB宽30米,则高压电线杆CD的高度为( )
,且AB=20米.身高1.7米的小明竖直站立于A点,眼睛在M点处测得竖立的高压电线杆顶端D点的仰角为24°,已知地面CB宽30米,则高压电线杆CD的高度为( )(结果精确到整数,参考数据:sin24°≈0.40,cos24°≈0.91,tan24°≈0.45)
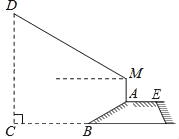
A. 30米 B. 32米 C. 34米 D. 36米
-
科目: 来源: 题型:
查看答案和解析>>【题目】王达和李力是八(2)班运动素质最好的两位同学,为了选出一名同学参加全校的体育运动大寒,班主任针对学校要测试的五个项目,对两位同学进行相应的测试(成绩:分),结果如下:
姓名
力量
速度
耐力
柔韧
灵敏
王达
60
75
100
90
75
李力
70
90
80
80
80
根据以上测试结果解答下列问题:
(1)补充完成下表:
姓名
平均成绩(分)
中位数(分)
众数(分)
方差(分2)
王达
80
75
75
190
李力
(2)任选一个角度分析推选哪位同学参加学校的比赛比较合适?并说明理由;
(3)若按力量:速度:耐力:柔韧:灵敏=1:2:3:3:1的比例折合成综合分数,推选得分同学参加比赛,请通过计算说明应推选哪位同学去参赛。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蛋糕店为了吸引顾客,在A、B两种蛋糕中,轮流降低其中一种蛋糕价格,这样形成两种盈利模式,模式一:A种蛋糕利润每盒8元,B种蛋糕利润每盒15元;模式二:A种蛋糕利润每盒14元,B种蛋糕利润每盒11元每天限定销售A、B两种蛋糕共40盒,且都能售完,设每天销售A种蛋糕x盒
(1)设按模式一销售A、B两种蛋糕所获利润为y1元,按模式二销售A、B两种蛋糕所获利润为y2元,分别求出y1、y2关于x的函数解析式;
(2)在同一个坐标系内分别画出(1)题中的两个函数的图象;

(3)若y始终表示y1、y2中较大的值,请问y是否为x的函数,并说说你的理由,并直接写出y的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我校4月份举办了教职工羽毛球赛,本次比赛共分三个项目:男双、女双和混双.比赛规定参赛男教师只能在男双或混双中选报一项,参赛女教师只能在女双或混双中选报一项,现将参赛人数和各项的参赛队数(两人组成一队)绘制成了如下不完整的统计图:
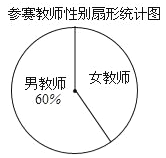
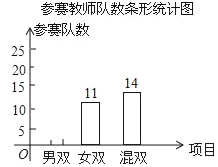
(1)本次比赛共有_____名参赛教师,并补全条形统计图;
(2)已知男双冠军分别是音乐教师和体育教师,女双冠军都是数学教师,混双冠军分别是数学男教师和美术女教师.暑假期问市教委将举办全市中小学教师羽毛球比赛,比赛规定:每所学校的参赛人数为两人,且参赛教师不得属于同一学科.所以学校决定:从三支冠军队伍中的数学教师中随机选取一人,再从其他教师中选取一人参加比赛.请用列表法或画树状图的方法求出所选两位教师恰好搭档参加混双项目的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.
(1)若AC=8cm,CB=6cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a,其它条件不变,你能猜想MN的长度吗?写出你的结论并说明理由;
(3)若点C在线段AB的延长线上,且满足AC-BC=b,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形并写出你的结论(不必说明理由).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只甲虫在 5×5 的方格(每小格边长为 1)上沿着网格线运动.它从 A处出发去看望 B、C、D 处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从 A 到 B 记为:A→B(+1,+4),从 B 到 A 记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)A→C( , ),B→C( , ),C→D ( , );
(2)若这只甲虫的行走路线为 A→B→C→D,请计算该甲虫走过的最少路程;
(3)若这只甲虫从 A 处去甲虫 P 处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出 P 的位置.

相关试题

