【题目】在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义:
“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.
例如:三点坐标分别为A(1,2),B(﹣3,1),C(2,﹣2),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.
(1)已知点A(1,2),B(﹣3,1),P(0,t).
①若A,B,P三点的“矩面积”为12,求点P的坐标;
②直接写出A,B,P三点的“矩面积”的最小值.
(2)已知点E(4,0),F(0,2),M(m,4m),N(n, ![]() ),其中m>0,n>0.
),其中m>0,n>0.
①若E,F,M三点的“矩面积”为8,求m的取值范围;
②直接写出E,F,N三点的“矩面积”的最小值及对应n的取值范围.
参考答案:
【答案】(1)①点P 的坐标为(0,﹣1);②A,B,P三点的“矩面积”的最小值为4;
(2)①∴0<m≤![]() ;②E,F,N三点的“矩面积”的最小值为16,此时n的取值范围为4≤n≤8.
;②E,F,N三点的“矩面积”的最小值为16,此时n的取值范围为4≤n≤8.
【解析】试题分析:(1)①首先由题意:a=4,然后分别从①当t>2时,h=t-1,当t<1时,h=2-t,去分析求解即可求得答案;
②首先根据题意得:h的最小值为:1,继而求得A,B,P三点的“矩面积”的最小值.
(2)①由E,F,M三点的“矩面积”的最小值为8,可得a=4,h=2,即可得![]() ,继而求得m的取值范围;
,继而求得m的取值范围;
②分别从当n≤4时,a=4,h=![]() ,当4<n<8时,a=n,h=
,当4<n<8时,a=n,h=![]() ,,当n≥8时,a=n,h=2,去分析求解即可求得答案;
,,当n≥8时,a=n,h=2,去分析求解即可求得答案;
试题解析:
解:(1)由题意:a=4.
①当t>2时,h=t﹣1,
则4(t﹣1)=12,可得t=4,故点P的坐标为(0,4);
当t<1时,h=2﹣t,
则4(2﹣t)=12,可得t=﹣1,故点P 的坐标为(0,﹣1);
②∵根据题意得:h的最小值为:1,
∴A,B,P三点的“矩面积”的最小值为4;
(2)①∵E,F,M三点的“矩面积”为8,
∴a=4,h=2,
∴![]() .
.
∴0≤m≤![]() .
.
∵m>0,
∴0<m≤![]() ;
;
②∵当n≤4时,a=4,h=![]() ,此时S=ah=
,此时S=ah=![]() ,
,
∴当n=4时,取最小值,S=16;
当4<n<8时,a=n,h=![]() ,此时S=ah=16;
,此时S=ah=16;
当n≥8时,a=n,h=2,此时S=ah=2n,
∴当n=8时,取最小值,S=16;
∴E,F,N三点的“矩面积”的最小值为16,此时n的取值范围为4≤n≤8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列性质中,矩形、菱形、正方形都具有的是( )
A. 对角线相等 B. 对角线互相垂直 C. 对角线平分一组对角 D. 对角线互相平分
-
科目: 来源: 题型:
查看答案和解析>>【题目】把文字翻译成数学符号,构建方程组模型是解此类题的关键某超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表统计了近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
5台
1800
第二周
6台
8台
3180
(1)求A、B两种型号的电风扇每台的销售价分别是多少元?
(2)若超市准备用不超过5250元的金额再采购这两种型号的电风扇共30台,
①求A种型号的电风扇最多能采购多少台?
②超市销售完这30台电风扇是否能实现利润不低于1240元的目标?若能实现,请写出相应的采购方案,若不能实现,请说明理由.
(进价、售价均保持不变,利润=销售收入﹣进货成本) -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学扩建教学楼,测量地基时,量得地基长为2a m,宽为(2a﹣24)m,试用a表示地基的面积,并计算当a=25时地基的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a>b,则下列各式中不能成立的是( )
A.a+3>b+3
B.a﹣4>b﹣4
C.2a>2b
D.﹣ >﹣
>﹣ 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于平移的说法正确的是( )
A. 经过平移,对应线段相等 B. 经过平移,对应角可能会改变
C. 经过平移,图形会改变 D. 经过平移,对应点所连的线段不相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:
(1)5 (2
(2 )+(3
)+(3 )(+4
)(+4 )
)
(2) (
(
 +
+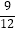 )×(24)
)×(24)
(3)(3)÷ ×
× ×(15)
×(15)
(4)-14+|(-2)3-10|-(-3)÷(-1)2017
相关试题

