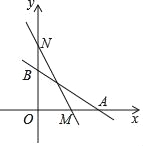
【题目】如图,直线:y=﹣![]() x+b与x轴分别交于A(4,0)、B两点,在y轴上有一点N(0,4),动点M从点A以每秒1个单位的速度匀速沿x轴向左移动.
x+b与x轴分别交于A(4,0)、B两点,在y轴上有一点N(0,4),动点M从点A以每秒1个单位的速度匀速沿x轴向左移动.
(1)点B的坐标为 ;
(2)求△MNO的面积S与移动时间t之间的函数关系式;
(3)当t= 时,△NOM≌△AOB;
(4)若M在x轴正半轴上,且△NOM≌△AOB,G是线段ON上一点,连结MG,将△MGN沿MG折叠,点N恰好落在x轴上的H处,求G点的坐标.
参考答案:
【答案】(1)(0,2)(2)S=|8﹣2t|(3)2或6(4)(0,![]() ﹣1)
﹣1)
【解析】
(1)由点A的坐标利用待定系数法可求出b值,再利用一次函数图象上点的坐标特征可求出点B的坐标;
(2)由点A、H的坐标及点M移动的速度可得出ON、OM的长度,再利用三角形的面积公式即可找出△MNO的面积S与移动时间t之间的函数关系式;
(3)由OA=ON=4、∠AOB=∠NOM=90°,可得出若要△NOM≌△AOB只需OM=OB=2,结合OM=|4﹣t|可得出关于t的含绝对值符号的一元一次方程,解之即可得出结论;
(4)设点G的坐标为(0,y),则OG=y,由折叠的性质可找出GH、OH的长度,在Rt△GOH中,利用勾股定理可得出关于y的一元一次方程,解之即可得出结论.
(1)∵直线y=﹣![]() x+b过点A(4,0),
x+b过点A(4,0),
∴0=﹣![]() ×4+b,解得:b=2,
×4+b,解得:b=2,
∴直线AB的函数关系式为y=﹣![]() x+2.
x+2.
当x=0时,y=﹣![]() x+2=2,
x+2=2,
∴点B的坐标为(0,2).
故答案为:(0,2).
(2)∵A(4,0),N(0,4),动点M从点A以每秒1个单位的速度匀速沿x轴向左移动,
∴OA=4,ON=4,OM=OA﹣AM=|4﹣t|,
∴S=![]() OMON=
OMON=![]() |4﹣t|×4=|8﹣2t|.
|4﹣t|×4=|8﹣2t|.
(3)∵OA=ON=4,∠AOB=∠NOM=90°,
∴若要△NOM≌△AOB,只需OM=OB=2.
∵OM=|4﹣t|,
∴|4﹣t|=2,
解得:t=2或6.
故答案为:2或6.
(4)设点G的坐标为(0,y),则OG=y.
根据折叠的性质,可知:MH=MN=![]() =2
=2![]() ,GH=GN=4﹣y,
,GH=GN=4﹣y,
∴OH=2![]() ﹣2.
﹣2.
在Rt△GOH中,GH2=OG2+OH2,即(4﹣y)2=y2+(2![]() ﹣2)2,
﹣2)2,
解得:y=![]() ﹣1,
﹣1,
∴点G的坐标为(0,![]() ﹣1).
﹣1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某一路口某一时段的汽车流量,小明同学10天中在同一时段统计通过该路口的汽车数量(单位:辆),将统计结果绘制成如下折线统计图:

由此估计一个月(30天)该时段通过该路口的汽车数量超过200辆的天数为( )
A.9
B.10
C.12
D.15 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题提出:如图已知直线OA的解析式是y=2x,OC⊥OA,求直线OC的函数解析式.
甲同学提出了他的想法:在直线y=2x上取一点M,过M作x轴的垂线,垂足为D设点M的横坐标为m,则点M的纵坐标为2m.即OD=m,MD=2m,然后在OC上截取ON=OM,过N作x轴的垂线垂足为B.则点N的坐标为 ,直线OC的解析式为 .
(2)拓展:已知直线OA的解析式是y=kx,OC⊥OA,求直线OC的函数解析式.
(3)应用:直接写出经过P(2,3),且垂直于直线y=﹣
 x+2的直线解析式 .
x+2的直线解析式 .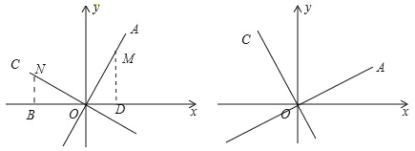
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知射线OM,ON,∠MON=45°点A在射线OM上,点B在射线ON上,OA=1,若△AOB是轴对称图形,点P为AB的中点,则OP2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】供电局的电力维修工要到30千米远的郊区进行电力抢修.技术工人骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果他们同时到达.已知抢修车的速度是摩托车的1.5倍,求这两种车的速度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两座城市的中心火车站A,B两站相距360km.一列动车与一列特快列车分别从A,B两站同时出发相向而行,动车的平均速度比特快列车快54km/h,当动车到达B站时,特快列车恰好到达距离A站135km处的C站.则动车的平均速度是 , 特快列车的平均速度是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定:一个数的平方等于-1,记作
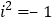 ,于是可知
,于是可知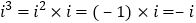
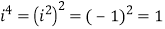 ……,按照这样的规律,
……,按照这样的规律,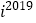 等于( )
等于( )A. 1B. -1C.
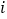 D.
D. 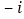
相关试题

