【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.

参考答案:
【答案】(1)证明见解析;
(2)点D在BC的中点上时,四边形ADCE是矩形.
【解析】
试题分析:(1)利用等边对等角以及平行四边形的性质可以证得∠EDC=∠ACB,则易证△ADC≌△ECD,利用全等三角形的对应边相等即可证得;
(2)根据平行四边形性质推出AE=BD=CD,AE∥CD,得出平行四边形,根据AC=DE推出即可.
试题解析:(1)证明:∵AB=AC,∴∠B=∠ACB,又∵ABDE中,AB=DE,AB∥DE,
∴∠B=∠EDC=∠ACB,AC=DE,
在△ADC和△ECD中, ,
,
∴△ADC≌△ECD(SAS).
(2)点D在BC的中点上时,四边形ADCE是矩形,∵四边形ABDE是平行四边形,
∴AE=BD,AE∥BC,∵D为边长中点,∴BD=CD,∴AE=CD,AE∥CD,
∴四边形ADCE是平行四边形,∵△ADC≌△ECD,∴AC=DE,
∴四边形ADCE是矩形,即点D在BC的中点上时,四边形ADCE是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.4m6÷2m3=2m2B.2x2+x3=3x5
C.(ab2)3=a3b5D.2a2a2=2a4
-
科目: 来源: 题型:
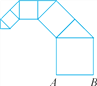
查看答案和解析>>【题目】按如图所示的方式作正方形和等腰直角三角形.若第一个正方形的边长AB=1,第一个正方形与第一个等腰直角三角形的面积和为S1,第二个正方形与第二个等腰直角三角形的面积和为S2……则第n个正方形与第n个等腰直角三角形的面积和Sn=____.
-
科目: 来源: 题型:
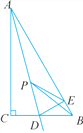
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠ABC=60°,D是BC边上的点,CD=1,将△ACD沿直线AD翻折,点C刚好落在AB边上的点E处.若P是直线AD上的动点,则△PEB的周长的最小值是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.
试说明:AC∥DF.将过程补充完整.
解:∵∠1=∠2( )
∠1=∠3( )
∴∠2=∠3()
∴∥ ( )
∴∠C=∠ABD ( )
又∵∠C=∠D()
∴∠D=∠ABD( )
∴AC∥DF( )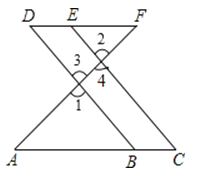
-
科目: 来源: 题型:
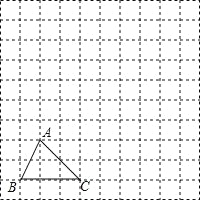
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(项点是网格线的交点).
(1)先将△ABC竖直向上平移6个单位,再水平向右平移3个单位得到△A1B1C1,请画出△A1B1C1;
(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2,请画出△A2B1C2;
(3)线段B1C1变换到B1C2的过程中扫过区域的面积为 .
相关试题

