【题目】如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.
试说明:AC∥DF.将过程补充完整.
解:∵∠1=∠2( )
∠1=∠3( )
∴∠2=∠3()
∴∥ ( )
∴∠C=∠ABD ( )
又∵∠C=∠D()
∴∠D=∠ABD( )
∴AC∥DF( )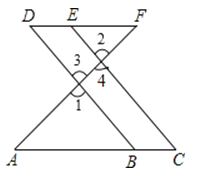
参考答案:
【答案】已知;对顶角相等;等量代换;BD;CE;同位角相等,两直线平行;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行
【解析】解:∵∠1=∠2( 已知),
∠1=∠3( 对顶角相等),
∴∠2=∠3( 等量代换),
∴BD∥CE( 同位角相等,两直线平行),
∴∠C=∠ABD ( 两直线平行,同位角相等),
又∵∠C=∠D( 已知),
∴∠D=∠ABD( 等量代换),
∴AC∥DF( 内错角相等,两直线平行),
故答案为:已知;对顶角相等;等量代换;BD;CE;同位角相等,两直线平行;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行.
由条件结合对顶角相等可证明BD∥CE,可得到∠C=∠ABD,再结合条件可得到∠D=∠ABD,可证明AC∥DF,据此填空即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按如图所示的方式作正方形和等腰直角三角形.若第一个正方形的边长AB=1,第一个正方形与第一个等腰直角三角形的面积和为S1,第二个正方形与第二个等腰直角三角形的面积和为S2……则第n个正方形与第n个等腰直角三角形的面积和Sn=____.
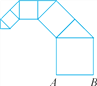
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠ABC=60°,D是BC边上的点,CD=1,将△ACD沿直线AD翻折,点C刚好落在AB边上的点E处.若P是直线AD上的动点,则△PEB的周长的最小值是______.
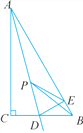
-
科目: 来源: 题型:
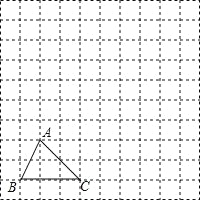
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(项点是网格线的交点).
(1)先将△ABC竖直向上平移6个单位,再水平向右平移3个单位得到△A1B1C1,请画出△A1B1C1;
(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2,请画出△A2B1C2;
(3)线段B1C1变换到B1C2的过程中扫过区域的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市平均每天产生垃圾700 t,由甲、乙两家垃圾处理厂处理.已知甲厂每小时可处理垃圾55 t,费用为550元;乙厂每小时可处理垃圾45 t,费用为495元.
(1)如果甲、乙两厂同时处理该城市的垃圾,那么每天需几小时?
(2)如果该城市规定每天用于处理垃圾的费用不得高于7370元,那么至少安排甲厂处理几小时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验探究:
(1)动手操作:
①如图1,将一块直角三角板DEF放置在直角三角板ABC上,使三角板DEF的两条直角边DE、DF分别经过点B、C,且BC∥EF,已知∠A=30°,则∠ABD+∠ACD=
②如图2,若直角三角板ABC不动,改变等腰直角三角板DEF的位置,使三角板DEF的两条直角边DE、DF仍然分别经过点B、C,那么∠ABD+∠ACD=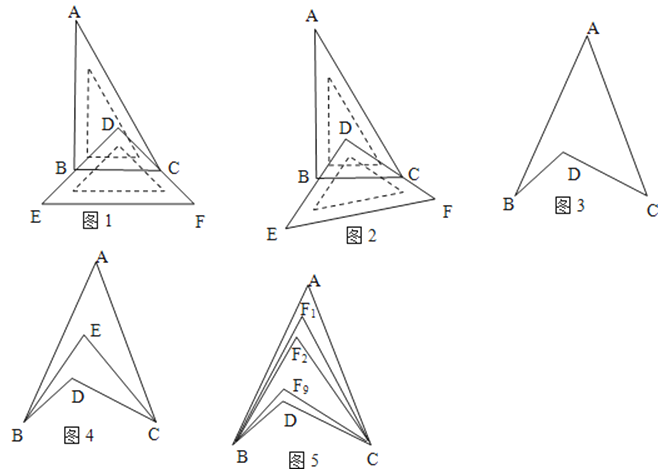
(2)猜想证明:
如图3,∠BDC与∠A、∠B、∠C之间存在着 关系
(3)灵活应用:
请你直接利用以上结论,解决以下列问题:
①如图4,BE平分∠ABD,CE平分∠ACB,若∠BAC=40°,∠BDC=120°,∠BEC
②如图5,∠ABD,∠ACD的10等分线相交于点F1、F2、…、F9 ,
若∠BDC=120°,∠BF3C=64°,则∠A的度数为
相关试题

