【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
参考答案:
【答案】C
【解析】试题解析:过E作EM∥BC,交AD于N,

∵AC=4,AE=2,
∴EC=2=AE,
∴AM=BM=2,
∴AM=AE,
∵AD是BC边上的中线,△ABC是等边三角形,
∴AD⊥BC,
∵EM∥BC,
∴AD⊥EM,
∵AM=AE,
∴E和M关于AD对称,
连接CM交AD于F,连接EF,
则此时EF+CF的值最小,
∵△ABC是等边三角形,
∴∠ACB=60°,AC=BC,
∵AM=BM,
∴∠ECF=![]() ∠ACB=30°,
∠ACB=30°,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一艘轮船在A,B两个码头之间航行,顺水航行需3h,逆水航行需5h.已知水流速度为4km/h,求轮船在静水中的航行速度.若设轮船在静水中的航行速度为xkm/h,则可列式为( )
A. 3x+4=5x﹣4 B. 3(4+x)=5(4﹣x)
C. 3(x+4)=5(x﹣4) D. 3(x﹣4)=5(x+4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,∠ADC+∠ABC=180°,有下列结论:①CD=CB;②AD+AB=2AE;③∠ACD=∠BCE;④AB-AD=2BE.其中正确的是( )

A. ② B. ①②③ C. ①②④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=24°,∠ACB=104°,AD⊥BC于D,AE平分∠BAC,求∠DAE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.4m6÷2m3=2m2B.2x2+x3=3x5
C.(ab2)3=a3b5D.2a2a2=2a4
-
科目: 来源: 题型:
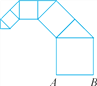
查看答案和解析>>【题目】按如图所示的方式作正方形和等腰直角三角形.若第一个正方形的边长AB=1,第一个正方形与第一个等腰直角三角形的面积和为S1,第二个正方形与第二个等腰直角三角形的面积和为S2……则第n个正方形与第n个等腰直角三角形的面积和Sn=____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.

相关试题

