Question

【题目】已知AB为⊙O直径，以OA为直径作⊙M．过B作⊙M得切线BC，切点为C，交⊙O于E．
（1）在图中过点B作⊙M作另一条切线BD，切点为点D（用尺规作图，保留作图痕迹，不写作法，不用证明）；
（2）证明：∠EAC=∠OCB；
（3）若AB=4，在图2中过O作OP⊥AB交⊙O于P，交⊙M的切线BD于N，求BN的值．

Answer 1

【答案】
（1）解：以MB为直径作圆，与⊙M相交于点D，直线BD即为另一条切线．
（2）证明：∵BC切圆与点C，

∴∠OCB=∠OAC，∠ECA=∠COA；

∵OA、AB分别为⊙M、⊙O的直径

∴∠AEC=∠ACO=90°，

∵∠EAC+∠ECA=90°，∠OAC+∠COA=90°，

∴∠EAC=∠OAC=∠OCB．

（3）解：连接DM，

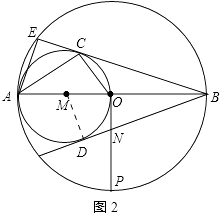
则∠BDM=90°在Rt△BDM中，BD=BC ．

∵△BON∽△BDM，

∴ ，

∴ ，

∴BN= ．

【解析】（1）以MB为直径作圆，与⊙M相交于点D，直线BD即为另一条切线．（2）根据BC切圆与点C，得到∠OCB=∠OAC、∠ECA=∠COA；再根据OA、AB分别为⊙M、⊙O的直径得到∠AEC=∠ACO=90°，从而得到∠EAC=∠OAC=OCB；（3）连接DM，则可以得到∠BDM=90°，然后利用△BON∽△BDM列出比例式求得BN的长即可．
【考点精析】掌握圆周角定理和切线的性质定理是解答本题的根本，需要知道顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径．