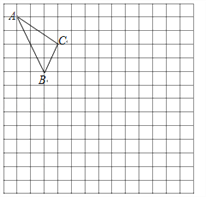
【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形![]() (顶点是网格线交点的三角形)的顶点
(顶点是网格线交点的三角形)的顶点![]() 的坐标分别是
的坐标分别是![]() .
.
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(3)请在![]() 轴上求作一点
轴上求作一点![]() ,使
,使![]() 的周长最小,并写出点
的周长最小,并写出点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)(2)见解析;(3)P(0,2).
【解析】分析:(1)根据A,C两点的坐标即可建立平面直角坐标系.
(2)分别作各点关于x轴的对称点,依次连接即可.
(3)作点C关于y轴的对称点C′,连接B1C′交y轴于点P,即为所求.
详解:(1)(2)如图所示:

(3)作点C关于y轴的对称点C′,连接B1C′交y轴于点P,则点P即为所求.
设直线B1C′的解析式为y=kx+b(k≠0),
∵B1(﹣2,-2),C′(1,4),
∴![]() ,解得:
,解得:![]() ,
,
∴直线AB2的解析式为:y=2x+2,
∴当x=0时,y=2,∴P(0,2).
-
科目: 来源: 题型:
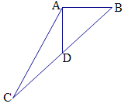
查看答案和解析>>【题目】如图,在△ABC中,AB=6,AC=10,BC边上的中线AD=4,则△ABC的面积为___________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.
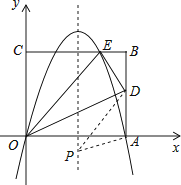
(1)求此抛物线的解析式;
(2)求AD的长;
(3)点P是抛物线对称轴上的一动点,当△PAD的周长最小时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点C1、C2、C3…在x轴上,点A1、A2、A3…在直线l上,A1(0,1),∠A2 A1B1=45°,则点Bn的坐标为____________(用n的代数式表示,n为正整数);

-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形
 中,
中, ,求
,求 的度数.(答案:
的度数.(答案: )
)例2 等腰三角形
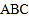 中,
中, ,求
,求 的度数.(答案:
的度数.(答案: 或
或 或
或 )
)张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形
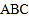 中,
中, ,求
,求 的度数.
的度数.(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,
 的度数不同,得到
的度数不同,得到 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形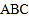 中,设
中,设 ,当
,当 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索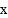 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(6,0),B(8,5),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)求对角线AC的长;
(2)设点D的坐标为(x,0),△ODC与△ABD的面积分别记为S1,S2.设S=S1﹣S2,写出S关于x的函数解析式,并探究是否存在点D使S与△DBC的面积相等?如果存在,用坐标形式写出点D的位置;如果不存在,说明理由.
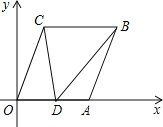
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,老师出示了如下的题目:如图(1),在等边△ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,试判断AE和BD的大小关系,并说明理由.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图(2),确定线段AE与DB的大小关系,请你直接写出结论:AE DB(填“>”,“<”或“=”);
(2)特例启发,解答题目
如图(1),试判断AE和BD的大小关系,并说明理由;
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC;若△ABC的边长为1,AE=2,请画出图形,求CD的长.

相关试题

