【题目】如图1,二次函数y= ![]() x2﹣2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.
x2﹣2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48. 
(1)求直线AB和直线BC的解析式;
(2)点P是线段AB上一点,点D是线段BC上一点,PD∥x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F.当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+ ![]() BH的值最小,求点H的坐标和GH+
BH的值最小,求点H的坐标和GH+ ![]() BH的最小值;
BH的最小值;
(3)如图2,直线AB上有一点K(3,4),将二次函数y= ![]() x2﹣2x+1沿直线BC平移,平移的距离是t(t≥0),平移后抛物线上点A,点C的对应点分别为点A′,点C′;当△A′C′K′是直角三角形时,求t的值.
x2﹣2x+1沿直线BC平移,平移的距离是t(t≥0),平移后抛物线上点A,点C的对应点分别为点A′,点C′;当△A′C′K′是直角三角形时,求t的值.
参考答案:
【答案】
(1)
解:∵点C是二次函数y= ![]() x2﹣2x+1图象的顶点,
x2﹣2x+1图象的顶点,
∴C(2,﹣1),
∵PE⊥x轴,BN⊥x轴,
∴△MAO∽△MBN,
∵S△AMO:S四边形AONB=1:48,
∴S△AMO:S△BMN=1:49,
∴OA:BN=1:7,
∵OA=1
∴BN=7,
把y=7代入二次函数解析式y= ![]() x2﹣2x+1中,可得7=
x2﹣2x+1中,可得7= ![]() x2﹣2x+1,
x2﹣2x+1,
∴x1=﹣2(舍),x2=6
∴B(6,7),
∵A的坐标为(0,1),
∴直线AB解析式为y=x+1,
∵C(2,﹣1),B(6,7),
∴直线BC解析式为y=2x﹣5.
(2)
解:如图1,
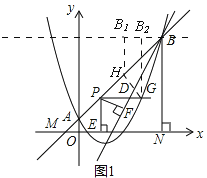
设点P(x0,x0+1),
∴D( ![]() ,x0+1),
,x0+1),
∴PE=x0+1,PD=3﹣ ![]() x0,
x0,
∵△PDF∽△BGN,
∴PF:PD的值固定,
∴PE×PF最大时,PE×PD也最大,
PE×PD=(x0+1)(3﹣ ![]() x0)=﹣
x0)=﹣ ![]() x02+
x02+ ![]() x0+3,
x0+3,
∴当x0= ![]() 时,PE×PD最大,
时,PE×PD最大,
即:PE×PF最大.此时G(5, ![]() )
)
∵△MNB是等腰直角三角形,
过B作x轴的平行线,
∴ ![]() BH=B1H,
BH=B1H,
GH+ ![]() BH的最小值转化为求GH+HB1的最小值,
BH的最小值转化为求GH+HB1的最小值,
∴当GH和HB1在一条直线上时,GH+HB1的值最小,
此时H(5,6),最小值为7﹣ ![]() =
= ![]()
(3)
解:令直线BC与x轴交于点I,
∴I( ![]() ,0)
,0)
∴IN= ![]() ,IN:BN=1:2,
,IN:BN=1:2,
∴沿直线BC平移时,横坐标平移m时,纵坐标则平移2m,平移后A′(m,1+2m),C′(2+m,﹣1+2m),
∴A′C′2=8,A′K2=5m2﹣18m+18,C′K2=5m2﹣22m+26,
当∠A′KC′=90°时,A′K2+KC′2=A′C′2,解得m= ![]() ,此时t=
,此时t= ![]() m=2
m=2 ![]() ±
± ![]() ;
;
当∠KC′A′=90°时,KC′2+A′C′2=A′K2,解得m=4,此时t= ![]() m=4
m=4 ![]() ;
;
当∠KA′C′=90°时,A′C′2+A′K2=KC′2,解得m=0,此时t=0.
【解析】(1)根据S△AMO:S四边形AONB=1:48,求出三角形相似的相似比为1:7,从而求出BN,继而求出点B的坐标,用待定系数法求出直线解析式.(2)先判断出PE×PF最大时,PE×PD也最大,再求出PE×PF最大时G(5, ![]() ),再简单的计算即可;(3)由平移的特点及坐标系中,两点间的距离公式得A′C′2=8,A′K2=5m2﹣18m+18,C′K2=5m2﹣22m+26,最后分三种情况计算即可.此题是二次函数综合题,主要考查了相似三角形的性质,待定系数法求函数解析式,两点间的结论公式,解本题的关键是相似三角形的性质的运用.
),再简单的计算即可;(3)由平移的特点及坐标系中,两点间的距离公式得A′C′2=8,A′K2=5m2﹣18m+18,C′K2=5m2﹣22m+26,最后分三种情况计算即可.此题是二次函数综合题,主要考查了相似三角形的性质,待定系数法求函数解析式,两点间的结论公式,解本题的关键是相似三角形的性质的运用.
【考点精析】掌握相似三角形的判定与性质是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近期猪肉价格不断走高,引起了民众与政府的高度关注.当市场猪肉的平均价格每千克达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.
(1)从今年年初至5月20日,猪肉价格不断走高,5月20日比年初价格上涨了60%.某市民在今年5月20日购买2.5千克猪肉至少要花100元钱,那么今年年初猪肉的最低价格为每千克多少元?
(2)5月20日,猪肉价格为每千克40元.5月21日,某市决定投入储备猪肉并规定其销售价在每千克40元的基础上下调a%出售.某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为每千克40元的情况下,该天的两种猪肉总销量比5月20日增加了a%,且储备猪肉的销量占总销量的 ,两种猪肉销售的总金额比5月20日提高了
,两种猪肉销售的总金额比5月20日提高了  a%,求a的值.
a%,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)=
 .例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所有3×4是12的最佳分解,所以F(12)=
.例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所有3×4是12的最佳分解,所以F(12)=  .
.
(1)如果一个正整数a是另外一个正整数b的平方,我们称正整数a是完全平方数.求证:对任意一个完全平方数m,总有F(m)=1;
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值. -
科目: 来源: 题型:
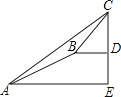
查看答案和解析>>【题目】已知△ABC是等腰直角三角形,∠BAC=90°,CD=
 BC,DE⊥CE,DE=CE,连接AE,点M是AE的中点.
BC,DE⊥CE,DE=CE,连接AE,点M是AE的中点. 
(1)如图1,若点D在BC边上,连接CM,当AB=4时,求CM的长;
(2)如图2,若点D在△ABC的内部,连接BD,点N是BD中点,连接MN,NE,求证:MN⊥AE;
(3)如图3,将图2中的△CDE绕点C逆时针旋转,使∠BCD=30°,连接BD,点N是BD中点,连接MN,探索 的值并直接写出结果.
的值并直接写出结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )
A.8.1米
B.17.2米
C.19.7米
D.25.5米 -
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣3,﹣1,
 ,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组
,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组  无解,且使关于x的分式方程
无解,且使关于x的分式方程  ﹣
﹣  =﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )
=﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )
A.﹣3
B.﹣2
C.﹣
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示,则乙到终点时,甲距终点的距离是米.

相关试题

