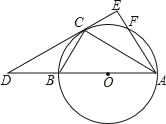
【题目】如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且点C是![]() 的中点,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
的中点,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
(1)求证:AE⊥DE;
(2)若∠BAF=60°,AF=4,求CE的长.
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】
试题(1)首先连接OC,由OC=OA,![]() ,易证得OC∥AE,又由DE切⊙O于点C,易证得AE⊥DE;
,易证得OC∥AE,又由DE切⊙O于点C,易证得AE⊥DE;
(2)由AB是⊙O的直径,可得△ABC是直角三角形,易得△AEC为直角三角形,根据AE=3求得AC的长,然后连接OF,可得△OAF为等边三角形,知AF=OA=![]() AB,在△ACB中,利用已知条件求得答案.
AB,在△ACB中,利用已知条件求得答案.
试题解析:(1)证明:连接OC,
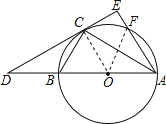
∵OC=OA,
∴∠BAC=∠OCA,
∵![]()
∴∠BAC=∠EAC,
∴∠EAC=∠OCA,
∴OC∥AE,
∵DE切⊙O于点C,
∴OC⊥DE,
∴AE⊥DE;
(2)解:∵AB是⊙O的直径,
∴△ABC是直角三角形,
∵∠CBA=60°,
∴∠BAC=∠EAC=30°,
∵△AEC为直角三角形,AE=3,
∴AC=2![]() ,
,
连接OF,
∵OF=OA,∠OAF=∠BAC+∠EAC=60°,
∴△OAF为等边三角形,
∴AF=OA=![]() AB,
AB,
在Rt△ACB中,AC=2![]() ,tan∠CBA=
,tan∠CBA=![]() ,
,
∴BC=2,
∴AB=4,
∴AF=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 两地相距30千米,甲骑自行车从
两地相距30千米,甲骑自行车从 地出发前往
地出发前往 地,乙在甲出发1小时后骑摩托车从
地,乙在甲出发1小时后骑摩托车从 地前往
地前往 地,图中的线段
地,图中的线段 和线段
和线段 分别反映了甲和乙所行使的路程
分别反映了甲和乙所行使的路程 (千米)与行使时间
(千米)与行使时间 (小时)的函数关系。
(小时)的函数关系。
请根据图像所提供的信息回答问题:
(1)乙骑摩托车的速度是每小时20 千米;
(2)两人的相遇地点与B地之间的距离是 千米;(3)求出甲所行使的路程
 (千米)与行使时间
(千米)与行使时间 (小时)的函数关系式,并写出
(小时)的函数关系式,并写出 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标中,点
 在第一象限内,
在第一象限内, 且
且 ,反比例函数
,反比例函数 的图像经过点
的图像经过点 ,
,
(1)当点
 的坐标为
的坐标为 时(如图),求这个反比例函数的解析式;
时(如图),求这个反比例函数的解析式;(2)当点
 在反比例函数
在反比例函数 的图像上,且在点
的图像上,且在点 的右侧时(如图2),用含字母
的右侧时(如图2),用含字母 的代数式表示点
的代数式表示点 的坐标;
的坐标;(3)在第(2)小题的条件下,求
 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有四个分别标有1、2、3、4的小球,它们的形状、大小等完全相同.小明先从口袋里随机不放回地取出一个小球,记下数字为x;小红在剩下有三个小球中随机取出一个小球,记下数字y.
(1)计算由x、y确定的点(x,y)在函数y=﹣x+6图象上的概率;
(2)小明、小红约定做一个游戏,其规则是:若x、y满足xy>6,则小明胜;若x、y满足xy<6,则小红胜.这个游戏规则公平吗?说明理由;若不公平,怎样修改游戏规则才对双方公平?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,AB、AD上各有一点P、Q,△APQ的周长为2,求∠PCQ.
为了解决这个问题,我们在正方形外以BC和AB延长线为边作△CBE,使得△CBE≌△CDQ(如图)
(1)△CBE可以看成由△CDQ怎样运动变化得到的?
(2)图中PQ与PE的长度有什么关系?为什么?
(3)请用(2)的结论证明△PCQ≌△PCE;
(4)根据以上三个问题的启发,求∠PCQ的度数.
(5)对于题目中的点Q,若Q恰好是AD的中点,求BP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,BD平分∠ABC,AD垂直于BD,△BCD的面积为45,△ADC的面积为20,则△ABD的面积为( ).

A.20B.18C.16D.25
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c经过点A(-1,0),点B(3,0)和点C(0,3).
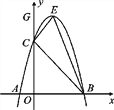
(1)求抛物线的解析式和顶点E的坐标;
(2)点C是否在以BE为直径的圆上?请说明理由;
(3)点Q是抛物线对称轴上一动点,点R是抛物线上一动点,是否存在点Q、R,使以Q、R、C、B为顶点的四边形是平行四边形?若存在,直接写出点Q、R的坐标,若不存在,请说明理由.
相关试题

