【题目】已知在平面直角坐标中,点![]() 在第一象限内,
在第一象限内,![]() 且
且![]() ,反比例函数
,反比例函数![]() 的图像经过点
的图像经过点![]() ,
,

(1)当点![]() 的坐标为
的坐标为![]() 时(如图),求这个反比例函数的解析式;
时(如图),求这个反比例函数的解析式;
(2)当点![]() 在反比例函数
在反比例函数![]() 的图像上,且在点
的图像上,且在点![]() 的右侧时(如图2),用含字母
的右侧时(如图2),用含字母![]() 的代数式表示点
的代数式表示点![]() 的坐标;
的坐标;
(3)在第(2)小题的条件下,求![]() 的值。
的值。
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)过A作AC⊥OB,根据三角形AOB为等腰直角三角形,得到AC=OC=BC=![]() OB,确定出A坐标,代入反比例解析式求出k的值,即可确定出反比例解析式;
OB,确定出A坐标,代入反比例解析式求出k的值,即可确定出反比例解析式;
(2)过A作AE⊥x轴,过B作BD⊥AE,利用同角的余角相等得到一对角相等,再由一对直角相等,且AO=AB,利用AAS得出三角形AOE与三角形ABD全等,由确定三角形的对应边相等得到BD=AE=n,AD=OE=m,进而表示出ED及OE+BD的长,即可表示出B坐标;
(3)由A与B都在反比例图象上,得到A与B横纵坐标乘积相等,列出关系式,变形后即可求出![]() 的值.
的值.
解:(1)如图1,过A作AC⊥OB,交x轴于点C,

∵OA=AB,∠OAB=90°,
∴△AOB为等腰直角三角形,
∴AC=OC=BC=![]() OB=3,
OB=3,
∴A(3,3),
将x=3,y=3代入反比例解析式得:3=![]() ,即k=9,
,即k=9,
则反比例解析式为y=![]() ;
;
(2)如图2,过A作AE⊥x轴,过B作BD⊥AE,
∵∠OAB=90°,
∴∠OAE+∠BAD=90°,
∵∠AOE+∠OAE=90°,
∴∠BAD=∠AOE,
在△AOE和△BAD中,

∴△AOE≌△BAD(AAS),
∴AE=BD=n,OE=AD=m,
∴DE=AE-AD=n-m,OE+BD=m+n,
则B(m+n,n-m);
(3)由A与B都在反比例图象上,得到mn=(m+n)(n-m),
整理得:n2-m2=mn,即(![]() )2+
)2+![]() -1=0,
-1=0,
这里a=1,b=1,c=-1,
∵△=1+4=5,
∴![]() =
=![]() ,
,
∵A(m,n)在第一象限,
∴m>0,n>0,
则![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少;
(4)如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一不透明的袋子中装有2个白球和1个红球,这些球除颜色不同外其余都相同,搅匀后,
(1)从中一次性摸出两只球,用树状图或列表表示其中一个是红球另一个是白球的所有结果并求其概率.
(2)向袋子中放入若干个红球(与原红球相同),搅匀后,从中任取一个球是红球的概率为
 ,求放入红球的个数.
,求放入红球的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 两地相距30千米,甲骑自行车从
两地相距30千米,甲骑自行车从 地出发前往
地出发前往 地,乙在甲出发1小时后骑摩托车从
地,乙在甲出发1小时后骑摩托车从 地前往
地前往 地,图中的线段
地,图中的线段 和线段
和线段 分别反映了甲和乙所行使的路程
分别反映了甲和乙所行使的路程 (千米)与行使时间
(千米)与行使时间 (小时)的函数关系。
(小时)的函数关系。
请根据图像所提供的信息回答问题:
(1)乙骑摩托车的速度是每小时20 千米;
(2)两人的相遇地点与B地之间的距离是 千米;(3)求出甲所行使的路程
 (千米)与行使时间
(千米)与行使时间 (小时)的函数关系式,并写出
(小时)的函数关系式,并写出 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有四个分别标有1、2、3、4的小球,它们的形状、大小等完全相同.小明先从口袋里随机不放回地取出一个小球,记下数字为x;小红在剩下有三个小球中随机取出一个小球,记下数字y.
(1)计算由x、y确定的点(x,y)在函数y=﹣x+6图象上的概率;
(2)小明、小红约定做一个游戏,其规则是:若x、y满足xy>6,则小明胜;若x、y满足xy<6,则小红胜.这个游戏规则公平吗?说明理由;若不公平,怎样修改游戏规则才对双方公平?
-
科目: 来源: 题型:
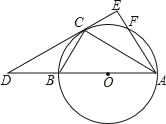
查看答案和解析>>【题目】如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且点C是
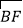 的中点,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
的中点,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.(1)求证:AE⊥DE;
(2)若∠BAF=60°,AF=4,求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,AB、AD上各有一点P、Q,△APQ的周长为2,求∠PCQ.
为了解决这个问题,我们在正方形外以BC和AB延长线为边作△CBE,使得△CBE≌△CDQ(如图)
(1)△CBE可以看成由△CDQ怎样运动变化得到的?
(2)图中PQ与PE的长度有什么关系?为什么?
(3)请用(2)的结论证明△PCQ≌△PCE;
(4)根据以上三个问题的启发,求∠PCQ的度数.
(5)对于题目中的点Q,若Q恰好是AD的中点,求BP的长.

相关试题

