【题目】如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据: ![]() ≈1.73,
≈1.73, ![]() ≈1.41.
≈1.41.
参考答案:
【答案】解:∵∠BEC=60°,∠BDE=30°,
∴∠DBE=60°﹣30°=30°,
∴BE=DE=20,
在Rt△BEC中,
BC=BEsin60°=20× ![]() =10
=10 ![]() ≈17.3(米),
≈17.3(米),
∴AB=BC﹣AC=17.3﹣12=5.3(米),
答:旗杆AB的高度为5.3米.
【解析】首先根据三角形外角的性质可得∠DBE=60°-30°=30°,根据等角对等边可得BE=DE,然后在Rt△BEC中,根据三角形函数可得BC=BEsin60°,进而可得BC长,然后可得AB的高度.
【考点精析】本题主要考查了关于仰角俯角问题的相关知识点,需要掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程或不等式组解应用题:
为进一步改善某市旅游景区公共服务设施,市政府预算用资金30万元在二百余家A级景区配备两种轮椅800台,其中普通轮椅每台350元,轻便型轮椅每台450元.
(1) 如果预算资金恰好全部用完,那么能购买两种轮椅各多少台?
(2) 由于获得了不超过5万元的社会捐助,那么轻便型轮椅最多可以买多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学阅读:
古希腊数学家海伦曾提出一个利用三角形三边之长求面积的公式:若一个三角形的三边长分别为a、b、c,则这个三角形的面积为
 ,其中
,其中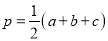 .这个公式称为“海伦公式”.
.这个公式称为“海伦公式”.数学应用:
如图1,在△ABC中,已知AB=9,AC=8,BC=7.
(1)请运用海伦公式求△ABC的面积;
(2)设AB边上的高为
 ,AC边上的高
,AC边上的高 ,求
,求 的值;
的值;(3)如图2,AD、BE为△ABC的两条角平分线,它们的交点为I,求△ABI的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,一次函数y=kx+b的图象与反比例函数
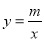 的图象交于
的图象交于 ,
,  两点.
两点.(1)求一次函数和反比例函数的解析式;
(2)设点
 和
和 是反比例函数
是反比例函数 图象上两点,若
图象上两点,若 ,求
,求 的值;
的值;(3)若M(x1,y1)和N(x2,y2)两点在直线AB上,如图2所示,过M、N两点分别作y轴的平行线交双曲线于E、F,已知﹣3<x1<0,x2>1,请探究当x1、x2满足什么关系时,MN∥EF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )

A. 13B. 16C. 8D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】在整式乘法的学习中,我们采用了构造几何图形的方法研究代数式的变形问题,借助直观、形象的几何图形,加深对整式乘法的认识和理解,感悟代数与几何的内在联系,现有边长分别为
 ,
, 的正方形Ⅰ号和Ⅱ号,以及长为
的正方形Ⅰ号和Ⅱ号,以及长为 ,宽为
,宽为 的长方形Ⅲ号,卡片足够多,我们可以选取适量的卡片拼接成几何图形.(卡片间不重叠、无缝隙)
的长方形Ⅲ号,卡片足够多,我们可以选取适量的卡片拼接成几何图形.(卡片间不重叠、无缝隙)根据已有的学习经验,解决下列问题:

(1)图1是由1张Ⅰ号卡片、1张Ⅱ号卡片、2张Ⅲ号卡片拼接成的正方形,那么这个几何图形表示的等式是______;

(2)小聪想用几何图形表示等式
 ,图2给出了他所拼接的几何图形的一部分,请你补全图形;
,图2给出了他所拼接的几何图形的一部分,请你补全图形;
(3)小聪选取2张Ⅰ号卡片、2张Ⅱ号卡片、5张Ⅲ号卡片拼接成一个长方形,请你画出拼接后的长方形,并直接写出几何图形表示的等式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:

(1)此次抽查的学生数为人;
(2)补全条形统计图;
(3)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是;
(4)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有人.
相关试题

