【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,![]() ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
(3)点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)m=﹣1或m=3时,四边形DMQF是平行四边形;(3)点Q的坐标为(3,2)或(﹣1,0)时,以点B、Q、M为顶点的三角形与△BOD相似.
x+2;(2)m=﹣1或m=3时,四边形DMQF是平行四边形;(3)点Q的坐标为(3,2)或(﹣1,0)时,以点B、Q、M为顶点的三角形与△BOD相似.
【解析】
(1)待定系数法求解可得;
(2)先利用待定系数法求出直线BD解析式为y=![]() x-2,则Q(m,-
x-2,则Q(m,-![]() m2+
m2+![]() m+2)、M(m,
m+2)、M(m,![]() m-2),由QM∥DF且四边形DMQF是平行四边形知QM=DF,据此列出关于m的方程,解之可得;
m-2),由QM∥DF且四边形DMQF是平行四边形知QM=DF,据此列出关于m的方程,解之可得;
(3)易知∠ODB=∠QMB,故分①∠DOB=∠MBQ=90°,利用△DOB∽△MBQ得![]() ,再证△MBQ∽△BPQ得
,再证△MBQ∽△BPQ得![]() ,即
,即![]() ,解之即可得此时m的值;②∠BQM=90°,此时点Q与点A重合,△BOD∽△BQM′,易得点Q坐标.
,解之即可得此时m的值;②∠BQM=90°,此时点Q与点A重合,△BOD∽△BQM′,易得点Q坐标.
(1)由抛物线过点A(-1,0)、B(4,0)可设解析式为y=a(x+1)(x-4),
将点C(0,2)代入,得:-4a=2,
解得:a=-![]() ,
,
则抛物线解析式为y=-![]() (x+1)(x-4)=-
(x+1)(x-4)=-![]() x2+
x2+![]() x+2;
x+2;
(2)由题意知点D坐标为(0,-2),
设直线BD解析式为y=kx+b,
将B(4,0)、D(0,-2)代入,得:
![]() ,解得:
,解得: ,
,
∴直线BD解析式为y=![]() x-2,
x-2,
∵QM⊥x轴,P(m,0),
∴Q(m,--![]() m2+
m2+![]() m+2)、M(m,
m+2)、M(m,![]() m-2),
m-2),
则QM=-![]() m2+
m2+![]() m+2-(
m+2-(![]() m-2)=-
m-2)=-![]() m2+m+4,
m2+m+4,
∵F(0,![]() )、D(0,-2),
)、D(0,-2),
∴DF=![]() ,
,
∵QM∥DF,
∴当-![]() m2+m+4=
m2+m+4=![]() 时,四边形DMQF是平行四边形,
时,四边形DMQF是平行四边形,
解得:m=-1(舍)或m=3,
即m=3时,四边形DMQF是平行四边形;
(3)如图所示:
∵QM∥DF,
∴∠ODB=∠QMB,
分以下两种情况:
①当∠DOB=∠MBQ=90°时,△DOB∽△MBQ,
则![]() ,
,
∵∠MBQ=90°,
∴∠MBP+∠PBQ=90°,
∵∠MPB=∠BPQ=90°,
∴∠MBP+∠BMP=90°,
∴∠BMP=∠PBQ,
∴△MBQ∽△BPQ,
∴![]() ,即
,即![]() ,
,
解得:m1=3、m2=4,
当m=4时,点P、Q、M均与点B重合,不能构成三角形,舍去,
∴m=3,点Q的坐标为(3,2);
②当∠BQM=90°时,此时点Q与点A重合,△BOD∽△BQM′,
此时m=-1,点Q的坐标为(-1,0);
综上,点Q的坐标为(3,2)或(-1,0)时,以点B、Q、M为顶点的三角形与△BOD相似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购进一批甲、乙两种办公桌若干张,并且每买1张办公桌必须买2把椅子,椅子每把100元,若学校购进20张甲种办公桌和15张乙种办公桌共花费24000元;购买10张甲种办公桌比购买5张乙种办公桌多花费2000元.
(1)求甲、乙两种办公桌每张各多少元?
(2)若学校购买甲乙两种办公桌共40张,且甲种办公桌数量不多于乙种办公桌数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三角形ABC中,AB=6,AC=BC=5,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF是⊙O的切线,D为切点,交CB的延长线于点E.
(1)求证:DF⊥AC;
(2)求tan∠E的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC与△ADE,AB=AC,AD=AE,且∠BAC=∠DAE=40°,CD与BE相交于点F,连接AF则下列结论:①CD=BE:②△ABF≌△ACF;③∠BFD=140°;④FA平分∠BFD;⑤∠FAC=∠FAE.其中正确的结论有( )

A.2个B.3个C.4个D.5个
-
科目: 来源: 题型:
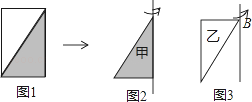
查看答案和解析>>【题目】如图1,把一张长10厘米、宽6厘米的长方形纸板分成两个相同的直角三角形.
(1)甲三角形(如图2)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方米?
(2)乙三角形(如图3)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】学完《全等三角形》知识后知道:满足“SSA”的两个三角形不一定全等,如图①,∠A与AB分别是△ABC与△ABD公共角与公共边,且AC=AD,但△ABC与△ABD不全等,但在特殊条件下“SSA”也可以确定两个三角形全等.如图②,∠MAB为锐角,AB=5,点B到射线AM的距离为3,点C在射线AM上,BC=x,当x的取值范围是__________时,△ABC的形状、大小是唯一确定。
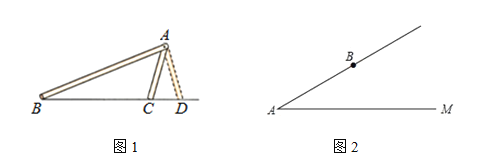
-
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形纸片
 按如图的方式折叠,得到菱形
按如图的方式折叠,得到菱形 ,若
,若 ,则
,则 的长为( )
的长为( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

