Question

【题目】如图，在四棱锥P﹣ABCD中，AD∥BC，∠ADC=∠PAB=90°，BC=CD= AD，E为AD的中点，异面直线AP与CD所成的角为90°．
（Ⅰ）证明：△PBE是直角三角形；
（Ⅱ）若二面角P﹣CD﹣A的大小为45°，求二面角A﹣PE﹣C的余弦值．

Answer 1

【答案】解：（Ⅰ）证明：如图，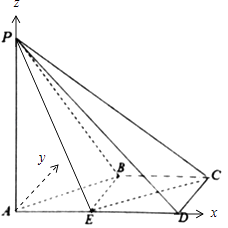
∵AD∥BC，AD=2BC，∴四边形ABCD为梯形，则AB与DC相交．
∵∠PAB=90°，∴PA⊥AB，
又异面直线AP与CD所成的角为90°，∴PA⊥CD．
∴PA⊥平面ABCD，则PA⊥BE．
∵AD∥BC，BC= ，
∴四边形BCDE为平行四边形，则BE∥CD．
∵∠ADC=90°，∴CD⊥AD，
∴BE⊥AD．
由BE⊥PA，BE⊥AD，PA∩AD=A，得BE⊥平面PAD，
∴BE⊥PE，则△PBE是直角三角形；
（Ⅱ）解：由（Ⅰ）知，CD⊥平面PAD，则∠PDA为二面角P﹣CD﹣A的平面角为45°，
设BC=1，则AD=PA=2．
在平面ABCD中，过A作Ay⊥AD．
以A为原点，分别以AD、Ay、AP所在直线为x、y、z轴建立空间直角坐标系．
则E（1，0，0），P（0，0，2），C（2，1，0）．
．
设平面PEC的一个法向量为 ．
由 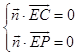，得 ，取z=1，得 ．
由图可知，平面PAE的一个法向量为 ．
∴cos＜ ＞= ．
∴二面角A﹣PE﹣C的余弦值为 ．
【解析】（Ⅰ）由已知证明PA⊥平面ABCD，得PA⊥BE．再由已知证明四边形BCDE为平行四边形，得BE∥CD．结合CD⊥AD，得BE⊥AD．再由线面垂直的判定得BE⊥平面PAD，进一步得到BE⊥PE，得到△PBE是直角三角形；（Ⅱ）由（Ⅰ）知，CD⊥平面PAD，则∠PDA为二面角P﹣CD﹣A的平面角为45°，设BC=1，得AD=PA=2．在平面ABCD中，过A作Ay⊥AD．以A为原点，分别以AD、Ay、AP所在直线为x、y、z轴建立空间直角坐标系．求得E，P，C的坐标，求出平面PEC与平面PAE的一个法向量，由两法向量所成角的余弦值可得二面角A﹣PE﹣C的余弦值．
【考点精析】关于本题考查的平面与平面垂直的性质，需要了解两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直才能得出正确答案．