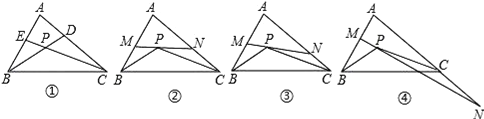
【题目】如图①,△ABC的角平分线BD,CE相交于点P.
(1)如果∠A=80,求∠BPC= .
(2)如图②,过点P作直线MN∥BC,分别交AB和AC于点M和N,试求∠MPB+∠NPC的度数(用含∠A的代数式表示) .
(3)将直线MN绕点P旋转。
(i)当直线MN与AB,AC的交点仍分别在线段AB和AC上时,如图③,试探索∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由。
(ii)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问(i)中∠MPB,∠NPC,∠A三者之间的数量关系是否仍然成立?若成立,请说明你的理由;若不成立,请给出∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由。

参考答案:
【答案】130°;
(2)90°﹣![]() ∠A
∠A
(3)(i)∠MPB+∠NPC=90°﹣![]() ∠A,理由见解析.
∠A,理由见解析.
(ii)不成立,有∠MPB﹣∠NPC=90°﹣![]() ∠A.
∠A.
理由见解析.
【解析】试题分析: (1)根据三角形内角和定理得到![]() ,再根据角平分线定义得到
,再根据角平分线定义得到![]() ,再利用三角形内角和定理得
,再利用三角形内角和定理得![]() ,然后把∠A的度数代入计算;
,然后把∠A的度数代入计算;
(2)根据平角定义得![]() ,然后根据(1)的求解;
,然后根据(1)的求解;
(3)( i)∠与(2)的说理一样;
(ⅱ)有结论![]() .
.
本题解析:(1) ![]()
![]()
![]()
![]()
![]() 故答案为:
故答案为: ![]()
(2)由![]() =
= ![]() 得∠MPB+∠NPC=
得∠MPB+∠NPC=![]() ∠BPC=
∠BPC=![]() 1(
1(![]() +
+![]() ∠A)=
∠A)= ![]()
![]() ∠A;故答案为:∠MPB+∠NPC=
∠A;故答案为:∠MPB+∠NPC=![]()
![]() ∠A.
∠A.
(3)(i)∠MPB+∠NPC=![]()
![]() ∠A.
∠A.
理由如下:
∵∠BPC=![]() +12∠
+12∠![]() A,
A,
∴∠MPB+∠NPC=![]() ∠BPC=180(
∠BPC=180(![]() +
+![]() ∠A)=
∠A)= ![]() 12
12![]() ∠A.
∠A.
(ii)不成立,有∠MPB∠NPC=![]()
![]() ∠A.
∠A.
理由如下:由题图④可知∠MPB+∠BPC∠NPC=![]() ,
,
由(1)知:∠BPC=![]() +
+![]() ∠A,∴∠MPB∠NPC=
∠A,∴∠MPB∠NPC=![]() ∠BPC=
∠BPC=![]() (
(![]() +
+![]() ∠A)=
∠A)= ![]()
![]() ∠A.
∠A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子中,不能成立的是( )
A. ﹣(﹣2)=2 B. ﹣|﹣2|=﹣2 C. 23=6 D. (﹣2)2=4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P的坐标(2a,6﹣a),且点P到两坐标轴的距离相等,则点P的坐标是( )
A.(12,﹣12)或(4,﹣4)
B.(﹣12,12)或(4,4)
C.(﹣12,12)
D.(4,4) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半圆中AB为直径,弦AC=CD=6
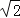 ,DE=EB=2,弧CDE的长度为 .
,DE=EB=2,弧CDE的长度为 .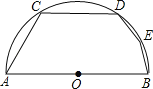
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某市九年级学生学业考试体育成绩,现随机抽取部分学生的体育(A:50分;B:49﹣45分;C:44﹣40分;D:39﹣30分;E:29﹣0分)成绩进行分段统计如下:

根据上面提供的信息,回答下列问题:
(1)在统计表中,a的值为 ,b的值为 ;
(2)将统计图补充完整;
(3)如果把成绩在40分以上(含40分)定为优秀,那么该市今年10560名九年级学生中体育成绩为优秀的学生人数约有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线相交于点O,PB∥AC,PC∥BD,PB、PC相交于点P.

(1)猜想四边形PCOB是什么四边形,并说明理由;
(2)当矩形ABCD满足什么条件时,四边形PCOB是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有若干张如图1的正方形硬纸片A.B和长方形硬纸片C.
(1)小明利用这些硬纸片拼成了如图2的一个新正方形,用两种不同的方法,计算出了新正方形的面积,由此,他得到了一个等式:_____________
(2)小明再取其中的若干张(三种纸片都取到)拼成一个面积为a2+nab+2b2长方形,则n可取的正整数值为____,并请在图3位置画出拼成的图形。
(3)根据拼图的经验,请将多项式a2+4ab+3b2分解因式:
相关试题

