Question

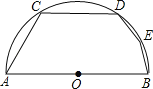
【题目】如图，在半圆中AB为直径，弦AC=CD=6，DE=EB=2，弧CDE的长度为 ．

Answer 1

【答案】

【解析】

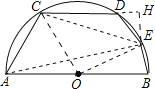
试题分析：过点E作EH⊥CD于H，连接OC、OE、AE，如图所示．根据弧、弦和圆周角的关系可得∠COE=90°，根据圆周角定理可得∠CAE=45°，再根据圆内接四边形对角互补及同角的补角相等可得∠HDE=45°，然后运用勾股定理可依次求出CE，CO，然后运用圆弧长公式就可解决问题．

解：过点E作EH⊥CD于H，连接OC、OE、AE，如图所示．

∵AC=CD，DE=EB，

∴，，

∴∠COE=∠AOB=90°，

∴∠CAE=45°．

∵∠CDE+∠CAE=180°，∠CDE+∠HDE=180°，

∴∠HDE=∠CAE=45°．

在Rt△DHE中，HE=DE×sin∠HDE=2×=，

DH=DE×cos∠HDE=2×=．

在Rt△CHE中，CE===10．

在Rt△COE中，CO=CE=5，

∴弧CDE的长度为=．

故答案为．