【题目】已知关于x的一元二次方程![]() 有实数根.
有实数根.
(1)求m的值;
(2)先作![]() 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求![]() 的最大值和最小值.
的最大值和最小值.
参考答案:
【答案】(1)1;(2)![]() ;(3)最大值为21,最小值为﹣4.
;(3)最大值为21,最小值为﹣4.
【解析】
试题(1)由题意△≥0,列出不等式,解不等式即可;
(2)画出翻折.平移后的图象,根据顶点坐标即可写出函数的解析式;
(3)首先确定n的取值范围,利用二次函数的性质即可解决问题;
试题解析:(1)对于一元二次方程![]() ,△=(m+1)2﹣2(m2+1)=﹣m2+2m﹣1=﹣(m﹣1)2,∵方程有实数根,∴﹣(m﹣1)2≥0,∴m=1.
,△=(m+1)2﹣2(m2+1)=﹣m2+2m﹣1=﹣(m﹣1)2,∵方程有实数根,∴﹣(m﹣1)2≥0,∴m=1.
(2)由(1)可知![]() =
=![]() ,图象如图所示:
,图象如图所示:
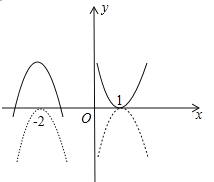
平移后的解析式为![]() ,即
,即![]() .
.
(3)由![]() 消去y得到
消去y得到![]() ,由题意△≥0,∴36﹣4n﹣8≥0,∴n≤7,∵n≤m,m=1,∴1≤n≤7,令y′=n2﹣4n=(n﹣2)2﹣4,∴n=2时,y′的值最小,最小值为﹣4,n=7时,y′的值最大,最大值为21,∴
,由题意△≥0,∴36﹣4n﹣8≥0,∴n≤7,∵n≤m,m=1,∴1≤n≤7,令y′=n2﹣4n=(n﹣2)2﹣4,∴n=2时,y′的值最小,最小值为﹣4,n=7时,y′的值最大,最大值为21,∴![]() 的最大值为21,最小值为﹣4.
的最大值为21,最小值为﹣4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
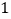 ,在平面直角坐标系中,二次函数
,在平面直角坐标系中,二次函数 的图象的顶点为
的图象的顶点为 点,与
点,与 轴交于
轴交于 点,与
点,与 轴交于
轴交于 、
、 两点,
两点, 点在原点的左侧,
点在原点的左侧, 点的坐标为
点的坐标为 ,
, ,
, .
.(
 )求这个二次函数的表达式.
)求这个二次函数的表达式.(
 )经过
)经过 、
、 两点的直线,与
两点的直线,与 轴交于点
轴交于点 ,在该抛物线上是否存在这样的点
,在该抛物线上是否存在这样的点 ,使以点
,使以点 、
、 、
、 、
、 为顶点的四边形为平行四边形?若存在,请求出点
为顶点的四边形为平行四边形?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.(
 )如图
)如图 ,若点
,若点 是该抛物线上一点,点
是该抛物线上一点,点 是直线
是直线 下方的抛物线上一动点,当点
下方的抛物线上一动点,当点 运动到什么位置时,
运动到什么位置时, 的面积最大?求出此时
的面积最大?求出此时 点的坐标和
点的坐标和 的最大面积.
的最大面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】画图题
(1)在图1中找出点A,使它到M,N两点的距离相等,并且到OH,OF的距离相等.
(2)如图2,①写出△ABC关于x轴对称的△A1B1C1的各顶点的坐标;
②画出△ABC关于y轴对称的△A2B2C2;
③在y轴上求作一点P,使△PBC的周长最小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC.
(2)写出AB+AC与AE之间的等量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长为4,D是直线BC上任一点,线段DA绕点D顺时针旋转60°得到线段DE,连接CE.

(1)当点D是BC的中点时,如图1,判断线段BD与CE的数量关系 ;
(2)当点D是BC边上任一点时,如图2,(1)中的结论是否仍然成立?请说明理由;
(3)当点D是BC延长线上一点且CD=1时,如图3,求线段CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图象与
的图象与 轴交于
轴交于 、
、 两点,与
两点,与 轴交于点
轴交于点 ,点
,点 的坐标为
的坐标为 ,且当
,且当 和
和 时二次函数的函数值
时二次函数的函数值 相等.
相等.(
 )求实数
)求实数 、
、 的值.
的值.(
 )如图
)如图 ,动点
,动点 、
、 同时从
同时从 点出发,其中点
点出发,其中点 以每秒
以每秒 个单位长度的速度沿
个单位长度的速度沿 边向终点
边向终点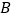 运动,点
运动,点 以每秒
以每秒 个单位长度的速度沿射线
个单位长度的速度沿射线 方向运动,当点
方向运动,当点 停止运动时,点
停止运动时,点 随之停止运动.设运动时间为
随之停止运动.设运动时间为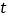 秒.连接
秒.连接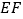 ,将
,将 沿
沿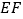 翻折,使点
翻折,使点 落在点
落在点 处,得到
处,得到 .
.①是否存在某一时刻
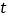 ,使得
,使得 为直角三角形?若存在,求出
为直角三角形?若存在,求出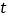 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.②设
 与
与 重叠部分的面积为
重叠部分的面积为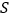 ,求
,求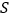 关于
关于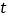 的函数关系式.
的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某二次函数的图象,将其向左平移
 个单位后的图象的函数解析式为
个单位后的图象的函数解析式为 ,则下列结论中正确的有( )
,则下列结论中正确的有( )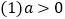 ;
; ;
; ;
; .
.
A.
 个 B.
个 B.  个 C.
个 C.  个 D.
个 D.  个
个
相关试题

