【题目】如图,等边△ABC的边长为4,D是直线BC上任一点,线段DA绕点D顺时针旋转60°得到线段DE,连接CE.

(1)当点D是BC的中点时,如图1,判断线段BD与CE的数量关系 ;
(2)当点D是BC边上任一点时,如图2,(1)中的结论是否仍然成立?请说明理由;
(3)当点D是BC延长线上一点且CD=1时,如图3,求线段CE的长.
参考答案:
【答案】(1)BD=CE;(2)仍然成立,理由详见解析;(3)5.
【解析】
(1)如图,连接AE,根据段AD绕点D顺时针旋转60°得到线段DE,得到AD=DE,推出△ADE是等边三角形,由△ABC是等边三角形,根据等边三角形的性质得到AB=AC证得AC垂直平分DE,根据线段垂直平分线的性质的即可得到结论;
(2)如图2,连接AE,由(1)得△ADE是等边三角形,得到AD=AE,∠DAE=60°,根据等边三角形的性质得到AB=AC,∠BAC=60°,证得∠BAD=∠CAE,推出△ABD≌△AEC,由全等三角形的性质得到BD=CE;
(3)如图3,连接AE,方法同(2).
解:(1)如图1中,连接AE,

∵段AD绕点D顺时针旋转60°得到线段DE,
∴AD=DE,
∵∠ADE=60°,
∴△ADE是等边三角形,
∵△ABC是等边三角形,
∴AB=AC,且BD=CD,
∴∠CAD=30°,
∴AC垂直平分DE,
∴CD=CE,
∴BD=CE,
故答案为:BD=CE;
(2)仍然成立,
理由如下:如图2,连接AE,

由(1)得△ADE是等边三角形,
∴AD=AE,∠DAE=60°,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠BAD=∠CAE,
在△ABD于△ACE中,

∴△ABD≌△AEC(SAS),
∴BD=CE,
(3)如图3,连接AE,

由(1)得△ADE是等边三角形,
∴AD=AE,∠DAE=60°,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠BAD=∠CAE,
在△ABD于△ACE中,

∴△ABD≌△AEC(SAS),
∴CE=BD,
∵BD=BC+CD=5,
∴CE=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】画图题
(1)在图1中找出点A,使它到M,N两点的距离相等,并且到OH,OF的距离相等.
(2)如图2,①写出△ABC关于x轴对称的△A1B1C1的各顶点的坐标;
②画出△ABC关于y轴对称的△A2B2C2;
③在y轴上求作一点P,使△PBC的周长最小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC.
(2)写出AB+AC与AE之间的等量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
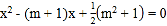 有实数根.
有实数根.(1)求m的值;
(2)先作
 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求
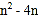 的最大值和最小值.
的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图象与
的图象与 轴交于
轴交于 、
、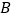 两点,与
两点,与 轴交于点
轴交于点 ,点
,点 的坐标为
的坐标为 ,且当
,且当 和
和 时二次函数的函数值
时二次函数的函数值 相等.
相等.(
 )求实数
)求实数 、
、 的值.
的值.(
 )如图
)如图 ,动点
,动点 、
、 同时从
同时从 点出发,其中点
点出发,其中点 以每秒
以每秒 个单位长度的速度沿
个单位长度的速度沿 边向终点
边向终点 运动,点
运动,点 以每秒
以每秒 个单位长度的速度沿射线
个单位长度的速度沿射线 方向运动,当点
方向运动,当点 停止运动时,点
停止运动时,点 随之停止运动.设运动时间为
随之停止运动.设运动时间为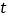 秒.连接
秒.连接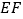 ,将
,将 沿
沿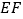 翻折,使点
翻折,使点 落在点
落在点 处,得到
处,得到 .
.①是否存在某一时刻
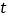 ,使得
,使得 为直角三角形?若存在,求出
为直角三角形?若存在,求出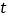 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.②设
 与
与 重叠部分的面积为
重叠部分的面积为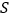 ,求
,求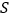 关于
关于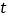 的函数关系式.
的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某二次函数的图象,将其向左平移
 个单位后的图象的函数解析式为
个单位后的图象的函数解析式为 ,则下列结论中正确的有( )
,则下列结论中正确的有( )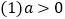 ;
; ;
; ;
; .
.
A.
 个 B.
个 B.  个 C.
个 C.  个 D.
个 D.  个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列叙述中,正确的是
A.直角三角形中,两边的平方和等于第三边的平方
B.如果一个三角形中两边的平方差等于第三边的平方,那么这个三角形是直角三角形
C.在
 中,
中, ,
, ,
,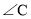 的对边分别为
的对边分别为  ,
,  ,
,  ,若
,若  ,则
,则
D.在
 中,
中,  ,
,  ,
, 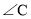 的对边分别为
的对边分别为  ,
,  ,
,  ,若
,若  ,则
,则 
相关试题

