【题目】如图![]() ,在平面直角坐标系中,二次函数
,在平面直角坐标系中,二次函数![]() 的图象的顶点为
的图象的顶点为![]() 点,与
点,与![]() 轴交于
轴交于![]() 点,与
点,与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() 点在原点的左侧,
点在原点的左侧,![]() 点的坐标为
点的坐标为![]() ,
,![]() ,
,![]() .
.
(![]() )求这个二次函数的表达式.
)求这个二次函数的表达式.
(![]() )经过
)经过![]() 、
、![]() 两点的直线,与
两点的直线,与![]() 轴交于点
轴交于点![]() ,在该抛物线上是否存在这样的点
,在该抛物线上是否存在这样的点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形?若存在,请求出点
为顶点的四边形为平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(![]() )如图
)如图![]() ,若点
,若点![]() 是该抛物线上一点,点
是该抛物线上一点,点![]() 是直线
是直线![]() 下方的抛物线上一动点,当点
下方的抛物线上一动点,当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积最大?求出此时
的面积最大?求出此时![]() 点的坐标和
点的坐标和![]() 的最大面积.
的最大面积.


参考答案:
【答案】(1) ![]() ;(2)存在点
;(2)存在点![]() ,坐标为
,坐标为![]() ;(3)
;(3)![]() ,
,![]() 最大为
最大为![]() .
.
【解析】
(1)求二次函数的表达式,需要求出A、B、C三点坐标.已知B点坐标,且OB=OC,可知C(0,3),![]() .则A坐标为(-1,0).将A,B,C三点坐标代入关系式,可求得二次函数的表达式.
.则A坐标为(-1,0).将A,B,C三点坐标代入关系式,可求得二次函数的表达式.
(2)已知抛物线关系式,求出顶点D坐标,求出直线CD,E是直线与x轴交点,可得E点坐标.四边形AECF为平行四边形,则![]() ,
,![]() ∥
∥![]() ,即可求出点F的坐标.
,即可求出点F的坐标.
(3)G在抛物线上,代入解析式求出G点坐标,过点![]() 作
作![]() 轴的平行线与
轴的平行线与![]() 交于点
交于点![]() ,设
,设![]() ,则
,则![]() ,可求出线段PQ的长度,
,可求出线段PQ的长度,![]() ,然后求当面积最大时x的值.
,然后求当面积最大时x的值.
(![]() )由已知得:
)由已知得:![]() ,
,![]() ,
,
将![]() ,
,![]() ,
,![]() 三点的坐标代入,得
三点的坐标代入,得 ,
,
∴![]() .
.
(![]() )存在.
)存在.
∵![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
∴![]() 点的坐标为
点的坐标为![]() ,
,
由![]() 、
、![]() 、
、![]() 、
、![]() 四点的坐标得:
四点的坐标得:![]() ,
,![]() ∥
∥![]() ,
,
∴以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点,的四边形为平移四边形,
为顶点,的四边形为平移四边形,
∴存在点![]() ,坐标为
,坐标为![]() .
.
(![]() )过点
)过点![]() 作
作![]() 轴的平行线与
轴的平行线与![]() 交于点
交于点![]() ,易得
,易得![]() ,直线
,直线![]() 为
为![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
当![]() 时,
时,![]() 最大,此时
最大,此时![]() ,
,![]() 最大为
最大为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )

A. 105° B. 110° C. 100° D. 120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】画图题
(1)在图1中找出点A,使它到M,N两点的距离相等,并且到OH,OF的距离相等.
(2)如图2,①写出△ABC关于x轴对称的△A1B1C1的各顶点的坐标;
②画出△ABC关于y轴对称的△A2B2C2;
③在y轴上求作一点P,使△PBC的周长最小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC.
(2)写出AB+AC与AE之间的等量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
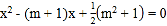 有实数根.
有实数根.(1)求m的值;
(2)先作
 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求
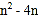 的最大值和最小值.
的最大值和最小值.
相关试题

