搜索
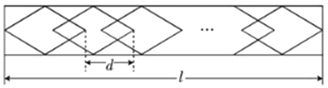
【题目】学校植物园沿路护栏的纹饰部分准备设计成若干个形状、大小完全相同的四边形图案，每平移一个图案，纹饰长度就增加
cm（如图）所示，已知每个四边形图案的水平方向的对角线长30cm．
（1）若=26cm，且该纹饰要用231个四边形图案，求纹饰的长度
；
（2）当=20cm时，若保持（1）中纹饰长度不变，则需要多少个这样的四边形图案？
参考答案：
【答案】（1）6010cm（2）300
【解析】
（1）根据纹饰的长度等于30+（n-1）d，可以解答本题；
（2）由（1）中求得的纹饰的长度和题目中的数据可以求得需要多少个这样的四边形图案．
（1）30+
=6010（cm）,
此时纹饰的长度为6010cm;
（2）
=300(个)．
答：需要300个这样的四边形图案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，射线AM∥BN，点E，F，D在射线AM上，点C在射线BN上，且∠BCD＝∠A，BE平分∠ABF，BD平分∠FBC.
(1)求证：AB∥CD.
(2)如果平行移动CD，那么∠AFB与∠ADB的比值是否发生变化？若变化，找出变化规律；若不变，求出这两个角的比值．
(3)如果∠A＝100°，那么在平行移动CD的过程中，是否存在某一时刻，使∠AEB＝∠BDC？若存在，求出此时∠AEB的度数；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知直线y=kx+b经过点A（5，0），B（1，4）．
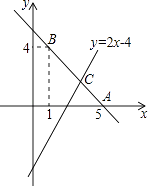
（1）求直线AB的解析式；
（2）若直线y=2x﹣4与直线AB相交于点C，求点C的坐标；
（3）根据图象，写出关于x的不等式2x﹣4＞kx+b的解集． -
科目： 来源： 题型：
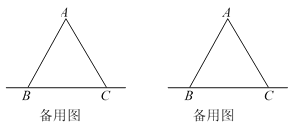
查看答案和解析>>【题目】在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
（1）如图1，当点D在线段BC上，如果∠BAC=90°，则∠BCE=_______度；
（2）如图2如果∠BAC=60°，则∠BCE=______度；
（3）设∠BAC=
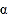，∠BCE=
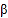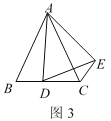
．①如图3，当点D在线段BC上移动，则
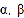之间有怎样的数量关系？请说明理由；②当点D在直线BC上移动，请直接写出
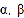之样的数量关系，不用证明。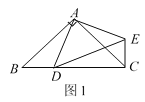
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，AD=2
，把边BC绕点B逆时针旋转30°得到线段BP，连接AP并延长交CD于点E，连接PC，则三角形PCE的面积为 ．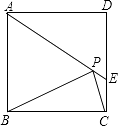 
-
科目： 来源： 题型：
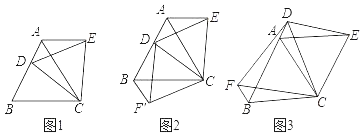
查看答案和解析>>【题目】（1）如图1，D是等边三角形ABC边BA上一动点（点D）与点B不重合，连接CD，以CD为边在BC上方作等边三角形DCE，连接AE，你能发现AE与BD之间的数量关系吗？并证明你发现的结论．
（2）如图二，当动点D在等边三角形ABC边BA上运动时（点D与点B不重合），连接DC，以DC为边在其上方、下方分别作等边三角形DCE和等边三角形DCF，连接AE，BF，探究AE，BF与AB有何数量关系？并证明你探究的结论．
（3）如图三，当动点D在等边三角形ABC边BA的延长线上运动时，其他作法与图2相同，若AE＝8，BF＝2，请直接写出AB＝ ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，∠1＝∠2，∠C＝∠D。
求证：∠A＝∠F。
证明：∵∠1＝∠2（已知），
又∠1＝∠DMN（_______________），
∴∠2＝∠_________（等量代换），
∴DB∥EC（ ），
∴∠DBC+∠C=1800（两直线平行 , ），
∵∠C＝∠D（ ），
∴∠DBC+ =1800（等量代换），
∴DF∥AC（ ，两直线平行），
∴∠A＝∠F( ）
相关试题
