【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)点P是x轴上的一动点,当PA+PB最小时,求点P的坐标;
(3)观察图象,直接写出不等式![]() 的解集.
的解集.

参考答案:
【答案】(1)反比例函数的解析式为![]() ;一次函数的解析式为y=-x+5;(2)点P的坐标为(
;一次函数的解析式为y=-x+5;(2)点P的坐标为(![]() ,0);(3)x<0或1≤x≤4
,0);(3)x<0或1≤x≤4
【解析】
(1)将点A(1,4)代入![]() 可得m的值,求得反比例函数的解析式;根据反比例函数解析式求得点B坐标,再由A、B两点的坐标可得一次函数的解析式;
可得m的值,求得反比例函数的解析式;根据反比例函数解析式求得点B坐标,再由A、B两点的坐标可得一次函数的解析式;
(2)作B关于x轴的对称点B′,连接AB′,交x轴于P,此时PA+PB=AB′最小,根据B的坐标求得B′的坐标,然后根据待定系数法求得直线AB′的解析式,进而求得与x轴的交点P即可.
(3)根据图象得出不等式![]() 的解集即可。
的解集即可。
解:(1)把A(1,4)代入![]() ,得:m=4,
,得:m=4,
∴反比例函数的解析式为![]() ;
;
把B(4,n)代入![]() ,得:n=1,
,得:n=1,
∴B(4,1),
把A(1,4)、(4,1)代入y=kx+b,
得:![]()
∴一次函数的解析式为y=-x+5;
(2)如图,作B关于x轴的对称点B′,连接AB′,交x轴于P,此时PA+PB=AB′最小,

∵B(4,1),
∴B′(4,-1),
设直线AB′的解析式为y=px+q,
![]()
解得
∴直线AB′的解析式为![]()
令y=0,得![]()
解得![]()
∴点P的坐标为(![]() ,0)
,0)
(3)根据图象得当x<0或1≤x≤4时,一次函数y=-x+5的图象在反比例函数![]() 的上方。
的上方。
∴不等式![]() 的解集为x<0或1≤x≤4。
的解集为x<0或1≤x≤4。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上两点A、B对应的数分别为-1、3,点P为数轴上一动点,其对应的数为x.

(1)若点P到点A、点B的距离相等,求点P对应的数;
(2)数轴上是否存在点P,使点P到点A、点B的距离之和为6?若存在,请求出x的值;若不存在,说明理由.
(3)点A、点B分别以2个单位长度/分、1个单位长度/分的速度向右运动,同时点P以6个单位长度/分的速度从O点向左运动.当遇到A时,点P立即以同样的速度向右运动,并不停地往返于点A与点B之间,求当点A与点B重合时,点P所经过的总路程是多少?
-
科目: 来源: 题型:
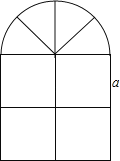
查看答案和解析>>【题目】窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长是acm,计算:
(1)窗户的面积;
(2)窗户的外框的总长.
-
科目: 来源: 题型:
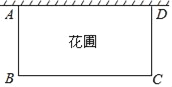
查看答案和解析>>【题目】为了美化生活环境,小兰的爸爸要在院墙外的一块空地上修建一个矩形花圃.如图所示,矩形花圃的一边利用长10米的院墙,另外三条边用篱笆围成,篱笆的总长为32米.设AB的长为x米,矩形花圃的面积为y平方米.
(1)用含有x的代数式表示BC的长,BC= ;
(2)求y与x的函数关系式,写出自变量x的取值范围;
(3)当x为何值时,y有最大值?最大值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=.
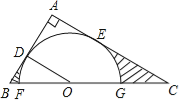
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把y=ax+b(其中a、b是常数,x、y是未知数)这样的方程称为“雅系二元一次方程”.当y=x时,“雅系二元一次方程y=ax+b”中x的值称为“雅系二元一次方程”的“完美值”.例如:当y=x时,“雅系二元一次方程”y=3x﹣4化为x=3x﹣4,其“完美值”为x=2.
(1)求“雅系二元一次方程”y=5x+6的“完美值”;
(2)x=3是“雅系二元一次方程”y=3x+m的“完美值”,求m的值;
(3)“雅系二元一次方程”y=kx+1(k≠0,k是常数)存在“完美值”吗?若存在,请求出其“完美值”,若不存在,请说明理由.
-
科目: 来源: 题型:
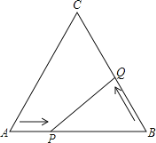
查看答案和解析>>【题目】如图,在边长为24cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟2cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟4cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求:
(1)经过6秒后,BP= cm,BQ= cm;
(2)经过几秒△BPQ的面积等于
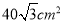 ?
? (3)经过几秒后,△BPQ是直角三角形?
相关试题

