搜索
【题目】如图，点F是
ABCD的边AD上的三等分点，BF交AC于点E，如果△AEF的面积为2，那么四边形CDFE的面积等于( )
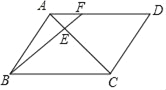
A. 18 B. 22 C. 24 D. 46
参考答案：
【答案】B
【解析】
连接FC，先证明△AEF∽△BEC，得出AE∶EC=1∶3，所以S△EFC=3S△AEF，在根据点F是□ABCD的边AD上的三等分点得出S△FCD=2S△AFC，四边形CDFE的面积=S△FCD+ S△EFC，再代入△AEF的面积为2即可求出四边形CDFE的面积.
∵AD∥BC，
∴∠EAF=∠ACB,∠AFE=∠FBC；
∵∠AEF=∠BEC，
∴△AEF∽△BEC，
∴
=
=
，
∵△AEF与△EFC高相等，
∴S△EFC=3S△AEF，
∵点F是□ABCD的边AD上的三等分点，
∴S△FCD=2S△AFC，
∵△AEF的面积为2，
∴四边形CDFE的面积=S△FCD+ S△EFC=16+6=22.
故答案选B.
-
科目： 来源： 题型：
查看答案和解析>>【题目】列方程解应用题：
某校八年级（一）班和（二）班的同学，在双休日参加修整花卉的实践活动．已知（一）班比（二）班每小时多修整2盆花，（一）班修整66盆花所用的时间与（二）班修整60盆花所用时间相等．（一）班和（二）班的同学每小时各修整多少盆花？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，为测量平地上一块不规则区域（图中的阴影部分）的面积，画一个边长为4m的正方形，使不规则区域落在正方形内．现向正方形内随机投掷小球（假设小球落在正方形内每一点都是等可能的），经过大量重复投掷试验，发现小球落在不规则区域的频率稳定在常数0.65附近，由此可估计不规则区域的面积约为（ ）
A. 2.6m2 B. 5.6m2 C. 8.25m2 D. 10.4m2
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，
和
都是等边三角形，且点
在
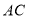上．（1）求证：
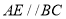
（2）直接写出
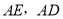和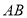
之间的关系；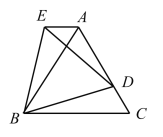
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料，回答问题：
两个含有二次根式的代数式相乘，如果它们的积不含有二次根式，我们就说这两个代数式互为有理化因式．例如：因为
，
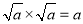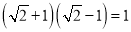，所
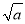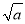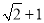与，
与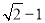
互为有理化因式．（1）
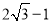的有理化因式是 ；（2）这样，化简一个分母含有二次根式的式子时，采用分子、分母同乘以分母的有理化因式的方法就可以了，例如：
，
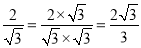用上述方法对
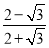进行分母有理化．（3）利用所需知识判断：若
，
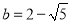，则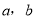
的关系是 ．（4）直接写结果：
． -
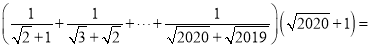科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知二次函数y=ax2+bx的图象与正比例函数y=kx的图象相交于点A（3，2），有下面四个结论：①ab＞0；②a﹣b＞﹣
；③sinα=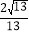
；④不等式kx≤ax2+bx的解集是0≤x≤3．其中正确的是（ ）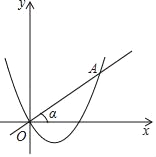
A. ①② B. ②③ C. ①④ D. ③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】某县九年级一模考试结束后，张老师依据一班考试成绩（单位：分）绘制了频数分布直方图（如图所示）
根据频数分布直方图，解答下列问题．
（1）填空：该班有_____人，根据直方图估算该班一模考试数学平均成绩是_____分；
（2）请在所给半径为2的圆中，画出成绩在70≤x＜80的人数对应的扇形，并求出该扇形的面积；
（3）从成绩在20≤x＜30和90≤x＜100的学生中任选2人，明明的成绩是91分，聪聪的成绩是28分，用树状图或列表法列出所有可能结果，并求明明、聪聪同时被选中的概率．
相关试题
