【题目】先阅读下面的材料,再回答后面的问题:
计算:10÷(![]() -
-![]() +
+![]() ).
).
解法一:原式=10÷![]() -10÷
-10÷![]() +10÷
+10÷![]() =10×2-10×3+10×6=50;
=10×2-10×3+10×6=50;
解法二:原式=10÷(![]() -
-![]() +
+![]() )=10÷
)=10÷![]() =10×3=30;
=10×3=30;
解法三:原式的倒数为(![]() -
-![]() +
+![]() )÷10
)÷10
=(![]() -
-![]() +
+![]() )×
)×![]() =
=![]() ×
×![]() -
-![]() ×
×![]() +
+![]() ×
×![]() =
=![]()
故原式=30.
(1)上面得到的结果不同,肯定有错误的解法,你认为解法 是错误的。
(2)请选择一种上述的正确方法解决下面的问题:
计算:(![]() )÷(
)÷(![]() ).
).
参考答案:
【答案】(1)一;(2)![]()
【解析】试题分析:上述得出的结果不同,肯定有错误的解法,我认为解法一是错误的.在正确的解法中,解法三最简捷,
利用乘法分配律求出原式倒数的值,即可求出原式的值.
试题解析: ![]() 上述得出的结果不同,肯定有错误的解法,我认为解法一是错误的.
上述得出的结果不同,肯定有错误的解法,我认为解法一是错误的.
故答案为:一.
(2)(选择一种正确的方法解答即可)(若用解法二)
原式=(![]() )÷(
)÷(![]() ),
),
=(![]() )÷
)÷![]() ,
,
![]()
![]()
(若用解法三)
原式的倒数为 (![]() )÷(
)÷(![]() ),
),
=(![]() )×(-28),
)×(-28),
![]() ,
,
![]()
![]()
故原式=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学校“争创美丽班级,争做文明学生”示范班级评比活动中,10位评委给九年级(1)班的评分情况如下表示:
评分(分)
75
80
85
90
评委人数
2
3
4
1
则这10位评委评分的平均数是( )
A.80分B.82分C.82.5分D.85分
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列多项式因式分解
(1)6a2+12ab+6b2
(2)2a(x2+4)2-32ax2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A. B.C三点,分别代表24,10,10,两只电子蚂蚁甲、乙分别从A.C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
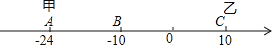
(1)甲、乙多少秒后相遇?
(2)甲出发多少秒后,甲到A. B.C三点的距离和为40个单位?
(3)当甲到A. B.C三点的距离和为40个单位时,甲调头原速返回,当甲、乙在数轴上再次相遇时,相遇点表示的数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
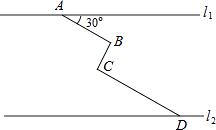
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:(12a3﹣6a2+3a)÷3a﹣1;(2)因式分解:﹣3x3+6x2y﹣3xy2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
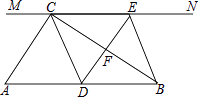
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
相关试题

