【题目】方程![]() ﹣3=
﹣3=![]() 的根,比关于x的方程2﹣
的根,比关于x的方程2﹣![]() (a﹣x)=2x的根的2倍还多4.5,求关于x的方程a(x﹣5)﹣2=a(2x﹣3)的解.
(a﹣x)=2x的根的2倍还多4.5,求关于x的方程a(x﹣5)﹣2=a(2x﹣3)的解.
参考答案:
【答案】x=-4.
【解析】
根据解方程,可得第一个方程的解,根据两个方程的解的关系,可得第二个方程的解,根据把方程的解代入方程,可得关于a的方程,根据解方程,可得a的值,把a的值代入方程a(x﹣5)﹣2=a(2x﹣3),可得关于x的一元一次方程,即可得答案.
解:![]() ﹣3=
﹣3=![]() ,解得x=
,解得x=![]() ,
,
方程![]() ﹣3=
﹣3=![]() 的根,比关于x的方程2﹣
的根,比关于x的方程2﹣![]() (a﹣x)=2x的根的2倍还多4.5,得
(a﹣x)=2x的根的2倍还多4.5,得
2﹣![]() (a﹣x)=2x的根是x=1.
(a﹣x)=2x的根是x=1.
把x=1代入方程2﹣![]() (a﹣x)=2x,得
(a﹣x)=2x,得
2﹣![]() (a﹣1)=2×1.
(a﹣1)=2×1.
解得a=1.
把a=1代入a(x﹣5)﹣2=a(2x﹣3),得
1![]() (x﹣5)﹣2=1
(x﹣5)﹣2=1![]() (2x﹣3).
(2x﹣3).
解得x=﹣4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD,∠C=90°,以AB为直径的⊙O交AD于点E,CD=ED,连接BD交⊙O于点F.
(1)求证:BC与⊙O相切;
(2)若BD=10,AB=13,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程.
(1)2(x﹣2)﹣3(4x﹣1)=9(1﹣x);
(2)
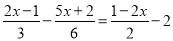 ;
;(3)
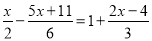 ;
;(4)
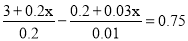 ;
; -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两公司同时销售一款进价为40元/千克的产品.图①中折线ABC表示甲公司销售价y1(元/千克)与销售量x(千克)之间的函数关系,图②中抛物线表示乙公司销售这款产品获得的利润y2(元)与销售量x(千克)之间的函数关系.


(1)分别求出图①中线段AB、图②中抛物线所表示的函数表达式;
(2)当该产品销售量为多少千克时,甲、乙两公司获得的利润的差最大?最大值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某条公共汽车线路收支差额
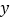 与乘客量
与乘客量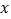 的函数关系如图所示(收支差额
的函数关系如图所示(收支差额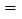 车票收入
车票收入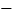 支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )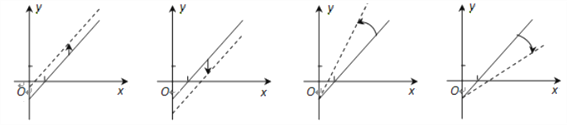
④ ③ ② ①
A. ①反映了建议(Ⅰ),③反映了建议(Ⅱ) B. ②反映了建议(Ⅰ),④反映了建议(Ⅱ)
C. ①反映了建议(Ⅱ),③反映了建议(Ⅰ) D. ②反映了建议(Ⅱ),④反映了建议(Ⅰ)
-
科目: 来源: 题型:
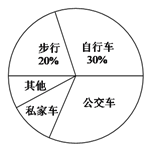
查看答案和解析>>【题目】某校为了解全校2400名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的频数分布直方图和扇形统计图(均不完整).
(1)这次调查中,一共抽取了多少名学生?
(2)补全频数分布直方图;
(3)估计全校所有学生中有多少人乘坐公交车上学.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的有( )
①用两颗钉子就可以把木条固定在墙上
②把笔尖看成一个点,当这个点运动时便得到一条线;
③把弯曲的公路改直,就能缩短路程;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上。
A.
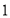 个B.
个B.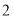 个C.
个C.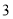 个D.
个D. 个
个
相关试题

