【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的图象经过原点O,交x轴于点A,其顶点B的坐标为(3,﹣ ![]() ).
).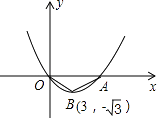
(1)求抛物线的函数解析式及点A的坐标;
(2)在抛物线上求点P,使S△POA=2S△AOB;
(3)在抛物线上是否存在点Q,使△AQO与△AOB相似?如果存在,请求出Q点的坐标;如果不存在,请说明理由.
参考答案:
【答案】
(1)
解:由函数图象经过原点得,函数解析式为y=ax2+bx(a≠0),
又∵函数的顶点坐标为(3,﹣ ![]() ),
),
∴ 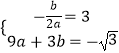 ,
,
解得: 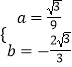 ,
,
故函数解析式为:y= ![]() x2﹣
x2﹣ ![]() x,
x,
由二次函数图象的对称性可得点A的坐标为(6,0)
(2)
解:∵S△POA=2S△AOB,
∴点P到OA的距离是点B到OA距离的2倍,即点P的纵坐标为2 ![]() ,
,
代入函数解析式得:2 ![]() =
= ![]() x2﹣
x2﹣ ![]() x,
x,
解得:x1=3+3 ![]() ,x2=3﹣3
,x2=3﹣3 ![]() ,
,
即满足条件的点P有两个,其坐标为:P1(3+3 ![]() ,2
,2 ![]() ),P2(3﹣3
),P2(3﹣3 ![]() ,2
,2 ![]() )
)
(3)
解:存在.
① 当点Q与点B重合时,满足△AQO与△AOB相似,
此时点Q的坐标为(3,﹣ ![]() );
);
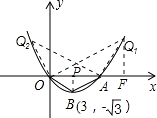
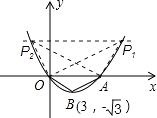
②当点Q与点B不重合时,
过点B作BP⊥OA,则tan∠BOP= ![]() =
= ![]() ,
,
故可得∠BOA=30°,
设Q1坐标为(x, ![]() x2﹣
x2﹣ ![]() x),过点Q1作Q1F⊥x轴,
x),过点Q1作Q1F⊥x轴,
∵△OAB∽△OQ1A,
∴∠Q1OA=30°,
故可得OF= ![]() Q1F,即x=
Q1F,即x= ![]() (
( ![]() x2﹣
x2﹣ ![]() x),
x),
解得:x=9或x=0(舍去),
经检验得此时OA=AQ1,△OQ1A是等腰三角形,且和△OBA相似.
即可得Q1坐标为(9,3 ![]() ),
),
根据函数的对称性可得Q2坐标为(﹣3,3 ![]() ).
).
∴在抛物线上存在点Q,使△AQO与△AOB相似,其坐标为:(3,﹣ ![]() )或(9,3
)或(9,3 ![]() )或(﹣3,3
)或(﹣3,3 ![]() )
)
【解析】(1)根据函数经过原点,可得c=0,然后根据函数的对称轴,及函数图象经过点(3,﹣ ![]() )可得出函数解析式,根据二次函数的对称性可直接得出点A的坐标.(2)根据题意可得点P到OA的距离是点B到OA距离的2倍,即点P的纵坐标为2
)可得出函数解析式,根据二次函数的对称性可直接得出点A的坐标.(2)根据题意可得点P到OA的距离是点B到OA距离的2倍,即点P的纵坐标为2 ![]() ,代入函数解析式可得出点P的横坐标;(3)分情况讨论,①点Q与点B重合可直接得出点Q的坐标;②点Q不与点B重合,先求出∠BOA的度数,然后可确定∠Q1OA=的度数,继而利用解直角三角形的知识求出x,得出Q1的坐标,利用二次函数图象函数的对称性可得出Q2的坐标.
,代入函数解析式可得出点P的横坐标;(3)分情况讨论,①点Q与点B重合可直接得出点Q的坐标;②点Q不与点B重合,先求出∠BOA的度数,然后可确定∠Q1OA=的度数,继而利用解直角三角形的知识求出x,得出Q1的坐标,利用二次函数图象函数的对称性可得出Q2的坐标.
【考点精析】认真审题,首先需要了解二次函数的图象(二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点),还要掌握二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用简便方法计算:
(1)(-3
 )+(+8
)+(+8 )-(-5
)-(-5 );
);(2)(-
 )+(+
)+(+ )+(+
)+(+ )+(-1
)+(-1 );
);(3)(-3
 )-(-
)-(- )+(-0.5)+3
)+(-0.5)+3 ;
;(4)(+3
 )+(-2
)+(-2 )-(-5
)-(-5 )-(+
)-(+ );
);(5)(-0.25)+(-3)-|-1
 |-(-3);
|-(-3);(6)(+
 )+(+17)+(-1
)+(+17)+(-1 )-(+7)-(-2
)-(+7)-(-2 )+(-
)+(- ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别
从A、C两点同时以1cm/s的相同的速度向C、A运动.

(1)四边形DEBF是平行四边形吗?说明你的理由.
(2)若BD=10cm,AC=16cm,当运动时间t为多少时,
四边形DEBF为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】加工一根轴,图上标明的直径加工要求是
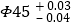 (单位:mm),则这种零件的标准尺寸是________mm,合格产品的最大直径是________mm,最小直径是________mm.如果加工成的轴的直径是44.8毫米,它是________(填“合格”或“不合格”)产品.
(单位:mm),则这种零件的标准尺寸是________mm,合格产品的最大直径是________mm,最小直径是________mm.如果加工成的轴的直径是44.8毫米,它是________(填“合格”或“不合格”)产品. -
科目: 来源: 题型:
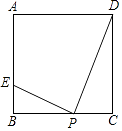
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠DPE=90°,PE交AB于点E,设BP=x,BE=y,则y关于x的函数图象大致是( )
A.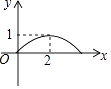
B.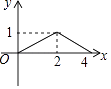
C.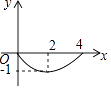
D.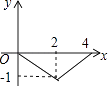
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的集合里:
2018,1,-1,-2014,0.5,
 ,-
,- ,-0.75,0,20%,
,-0.75,0,20%,
整数集合:{____________________…};正分数集合:{________________…};
负分数集合:{________________…};正数集合:{__________________…};
负数集合:{__________________…}.
相关试题

