【题目】如图,正方形ABCD的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠DPE=90°,PE交AB于点E,设BP=x,BE=y,则y关于x的函数图象大致是( )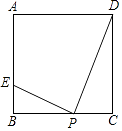
A.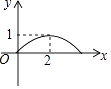
B.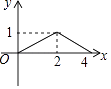
C.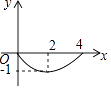
D.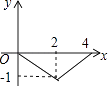
参考答案:
【答案】A
【解析】解:∵四边形ABCD是正方形,
∴∠B=∠C=90°
∵PE⊥DP,
∴∠DPC+∠EPB=90°,∠BPE+∠PEB=180°﹣∠B=90°
∴∠DPC=∠BEP,又∠B=∠CBAP=∠QPC
∴△EBP∽△PCD,
∴ ![]() =
= ![]() ,又BP=x,PC=BC﹣BP=4﹣x,CD=4,BE=y,
,又BP=x,PC=BC﹣BP=4﹣x,CD=4,BE=y,
即 ![]() =
= ![]() ,
,
∴y=﹣ ![]() x2+x(0<x<4),
x2+x(0<x<4),
故选A.
【考点精析】本题主要考查了函数的图象和相似三角形的应用的相关知识点,需要掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值;测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的图象经过原点O,交x轴于点A,其顶点B的坐标为(3,﹣
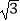 ).
).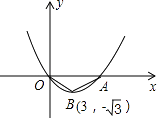
(1)求抛物线的函数解析式及点A的坐标;
(2)在抛物线上求点P,使S△POA=2S△AOB;
(3)在抛物线上是否存在点Q,使△AQO与△AOB相似?如果存在,请求出Q点的坐标;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】加工一根轴,图上标明的直径加工要求是
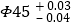 (单位:mm),则这种零件的标准尺寸是________mm,合格产品的最大直径是________mm,最小直径是________mm.如果加工成的轴的直径是44.8毫米,它是________(填“合格”或“不合格”)产品.
(单位:mm),则这种零件的标准尺寸是________mm,合格产品的最大直径是________mm,最小直径是________mm.如果加工成的轴的直径是44.8毫米,它是________(填“合格”或“不合格”)产品. -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的集合里:
2018,1,-1,-2014,0.5,
 ,-
,- ,-0.75,0,20%,
,-0.75,0,20%,
整数集合:{____________________…};正分数集合:{________________…};
负分数集合:{________________…};正数集合:{__________________…};
负数集合:{__________________…}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,则BD=(提示:可连接BE)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AGF=∠ABC,∠1+∠2=180°,
(1)求证;BF∥DE.
(2)如果DE⊥AC于点E,∠2=150°,求∠AFG的度数.

相关试题

