【题目】已知关于![]() 的方程
的方程![]() 有两个正整数根(
有两个正整数根(![]() 是正整数).
是正整数).![]() 的三边
的三边![]() 、
、![]() 、
、![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
求:
![]() 的值;
的值;
![]() 的面积.
的面积.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)已知关于![]() 的方程
的方程![]() 有两个正整数根(
有两个正整数根(![]() 是整数),由此即可得
是整数),由此即可得![]() ,设
,设![]() ,
,![]() 是此方程的两个根,根据根与系数的关系可得
是此方程的两个根,根据根与系数的关系可得![]() ,因为
,因为![]() 也是正整数,即可得
也是正整数,即可得![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() ,再由
,再由![]() 为正整数,即可得
为正整数,即可得![]() ;(2)由(1)得出的m的值,然后将
;(2)由(1)得出的m的值,然后将![]() ,
,![]() 进行化简,得出a,b的值.然后再根据三角形三边的关系来确定符合条件的a,b的值,进而得出三角形的面积.
进行化简,得出a,b的值.然后再根据三角形三边的关系来确定符合条件的a,b的值,进而得出三角形的面积.
![]() ∵关于
∵关于![]() 的方程
的方程![]() 有两个正整数根(
有两个正整数根(![]() 是整数).
是整数).
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,
,![]() 是此方程的两个根,
是此方程的两个根,
∴![]() ,
,
∴![]() 也是正整数,即
也是正整数,即![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() ,
,
又![]() 为正整数,
为正整数,
∴![]() ;
;
![]() 把
把![]() 代入两等式,化简得
代入两等式,化简得![]() ,
,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]() 、
、![]() 是方程
是方程![]() 的两根,而
的两根,而![]() ,由韦达定理得
,由韦达定理得![]() ,
,![]() ,则
,则![]() 、
、![]() .
.
①![]() ,
,![]() 时,由于
时,由于![]()
故![]() 为直角三角形,且
为直角三角形,且![]() ,
,![]() .
.
②![]() ,
,![]() 时,因
时,因![]() ,故不能构成三角形,不合题意,舍去.
,故不能构成三角形,不合题意,舍去.
③![]() ,
,![]() 时,因
时,因![]() ,故能构成三角形.
,故能构成三角形.
![]()
综上,![]() 的面积为
的面积为![]() 或
或![]() .
.
-
科目: 来源: 题型:
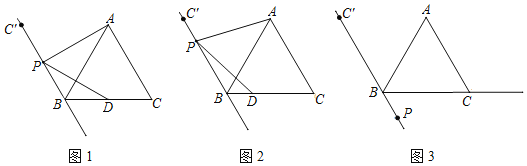
查看答案和解析>>【题目】△ABC是等边三角形,点C关于AB对称的点为C′,点P是直线C′B上的一个动点,连接AP,作∠APD=60°交射线BC于点D.
(1)若点P在线段C′B上(不与点C′,点B重合)
①如图1,当点P是线段C′B的中点时,直接写出线段PD与线段PA的数量关系 .
②如图2,点P是线段C′B上任意一点,证明PD与PA的数量关系.
(2)若点P在线段C′B的延长线上,
①依题意补全图3;
②直接写出线段BD,AB,BP之间的数量关系为: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个矩形铁片,长是
 ,宽是
,宽是 ,中间挖去
,中间挖去 的矩形,剩下的铁框四周一样宽,若设宽度为
的矩形,剩下的铁框四周一样宽,若设宽度为 ,那么挖去的矩形长是________
,那么挖去的矩形长是________ ,宽是________
,宽是________ ,根据题意可得方程________.
,根据题意可得方程________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在长方形纸片ABCD中,AB=32cm,把长方形纸片沿AC折叠,点B落在点E处,AE交DC于点F,AF=25cm,则AD的长为( )

A. 16cm B. 20cm C. 24cm D. 28cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程x2﹣4x+k=0有两个不相等的实数根
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句:①-1是1的平方根。②带根号的数都是无理数。③-1的立方根是-1。④
 的立方根是2。⑤(-2)2的算术平方根是2。⑥-125的立方根是±5。⑦有理数和数轴上的点一一对应。其中正确的有( )
的立方根是2。⑤(-2)2的算术平方根是2。⑥-125的立方根是±5。⑦有理数和数轴上的点一一对应。其中正确的有( )A. 2个B. 3个C. 4个D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形ABCD的顶点坐标分别为A(﹣2,1),B(﹣4,1),C(﹣3,2),D(﹣1,2).

(1)在图中画出四边形ABCD,并求出四边形ABCD的面积;
(2)在图中画出四边形ABCD关于x轴的对称图形A1B1C1D1,并分别写出点A、C的对应点A1、C1的坐标.
相关试题

