【题目】四边形ABCD是正方形,对角线AC,BD相交于点O.
(1)如图1,点P是正方形ABCD外一点,连接OP,以OP为一边,作正方形OPMN,且边ON与边BC相交,连接AP,BN.
①依题意补全图1;
②判断AP与BN的数量关系及位置关系,写出结论并加以证明;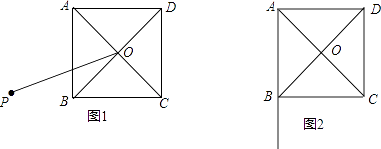
(2)点P在AB延长线上,且∠APO=30°,连接OP,以OP为一边,作正方形OPMN,且边ON与BC的延长线恰交于点N,连接CM,若AB=2,求CM的长(不必写出计算结果,简述求CM长的过程)
参考答案:
【答案】
(1)
解:①补全图形如图1所示,
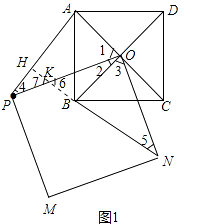
②结论:AP=BN,AP⊥BN.
理由:延长NB交AP于H,交OP于K.
∵四边形ABCD是正方形,
∴OA=OB,AO⊥BO,
∴∠1+∠2=90°,
∵四边形OPMN是正方形,
∴OP=ON,∠PON=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
在△APO和△BNO中,
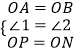 ,
,
∴△APO≌△BNO,
∴AP=BN,∴∠4=∠5,
在△OKN中,∠5+∠6=90°,
∵∠7=∠6,
∴∠4+∠7=90°,
∴∠PHK=90°,
∴AP⊥BN.
(2)
解:解题思路如下:
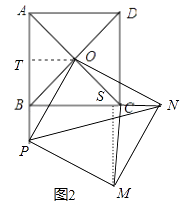
a.首先证明△APO≌△BNO,AP=BN,∠OPA=ONB.
b.作OT⊥AB于T,MS⊥BC于S,由题意可知AT=TB=1,
c.由∠APO=30°,可得PT= ![]() ,BN=AP=
,BN=AP= ![]() +1,可得∠POT=∠MNS=60°.
+1,可得∠POT=∠MNS=60°.
d.由∠POT=∠MNS=60°,OP=MN,
可证,△OTP≌△NSM,
∴PT=MS= ![]() ,
,
∴CN=BN﹣BC= ![]() ﹣1,
﹣1,
∴SC=SN﹣CN=2﹣ ![]() ,
,
在RT△MSC中,CM2=MS2+SC2,
∴MC的长可求.
【解析】(1)①根据题意作出图形即可.②结论:AP=BN,AP⊥BN,只要证明△APO≌△BNO即可.(2)在RT△CMS中,求出SM,SC即可解决问题.
【考点精析】认真审题,首先需要了解正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E,A,C在一条直线上.给出下列三个事项:①AD⊥BC,EG⊥BC,垂足分别为D,G;②∠1=∠2;③AD平分∠BAC.
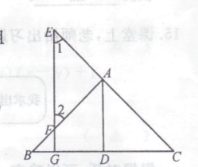
(1)以其中两个事项作为条件,另一个事项作为结论,你能组成个正确的结论;
(2)请你选择其中一个正确的结论进行说明理由.解:以为条件,为结论.(填写序号)理由是: -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示,则乙到终点时,甲距终点的距离是 米.
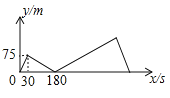
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的一元二次方程mx2﹣3(m﹣1)x+2m﹣3=0(m>3).
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两个实数根分别为x1 , x2(用含m的代数式表示);
①求方程的两个实数根x1 , x2(用含m的代数式表示);
②若mx1<8﹣4x2 , 直接写出m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:8101×0.125100=
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)x2﹣6x+5=0
(2)2x2﹣3x﹣1=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的方程3x-m+1=2x-1的解是负数,那么m的取值范围是( )
A. m>0 B. m<0 C. m>2 D. m<2
相关试题

