【题目】已知:关于x的一元二次方程mx2﹣3(m﹣1)x+2m﹣3=0(m>3).
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两个实数根分别为x1 , x2(用含m的代数式表示);
①求方程的两个实数根x1 , x2(用含m的代数式表示);
②若mx1<8﹣4x2 , 直接写出m的取值范围.
参考答案:
【答案】
(1)证明:∵mx2﹣3(m﹣1)x+2m﹣3=0(m>3)是关于x的一元二次方程,
∴△=[(﹣3(m﹣1)]2﹣4m(2m﹣3)=m2﹣6m+9=(m﹣3)2,
∵m>3,
∴(m﹣3)2>0,即△>0,
∴方程总有两个不相等的实数根
(2)①由求根公式得x= ![]() ,
,
∴x=1,或x= ![]() ,
,
∵m>3,
∴ ![]() >3,
>3,
当x1<x2,
∴x1=1,x2=2﹣ ![]() ;
;
当x1>x2,
这种情况不存在;
∴x1=1,x2=2﹣ ![]() ;
;
②∵mx1<8﹣4x2,
∴m<8﹣4(2﹣ ![]() ),
),
解得:3<m<2 ![]() .
.
【解析】(1)由于m>3,此方程为关于x的一元二次方程,再计算出判别式△=(m﹣3)2 , 然后根据判别式的意义即可得到结论;(2)②由求根公式得到x=1,或x= ![]() ,即可得到结论;②根据mx1<8﹣4x2 , 即可得到 结果.
,即可得到结论;②根据mx1<8﹣4x2 , 即可得到 结果.
【考点精析】根据题目的已知条件,利用求根公式和根与系数的关系的相关知识可以得到问题的答案,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于函数y=-3x,判断正确的是( )
A. 图象经过点(0,0)和点(-1,-3)
B. 图象经过第一、三象限
C. y随x的增大而减小
D. 图象是一条射线
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E,A,C在一条直线上.给出下列三个事项:①AD⊥BC,EG⊥BC,垂足分别为D,G;②∠1=∠2;③AD平分∠BAC.
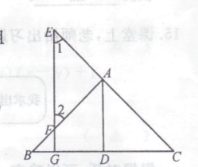
(1)以其中两个事项作为条件,另一个事项作为结论,你能组成个正确的结论;
(2)请你选择其中一个正确的结论进行说明理由.解:以为条件,为结论.(填写序号)理由是: -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示,则乙到终点时,甲距终点的距离是 米.
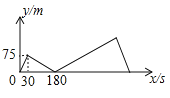
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是正方形,对角线AC,BD相交于点O.
(1)如图1,点P是正方形ABCD外一点,连接OP,以OP为一边,作正方形OPMN,且边ON与边BC相交,连接AP,BN.
①依题意补全图1;
②判断AP与BN的数量关系及位置关系,写出结论并加以证明;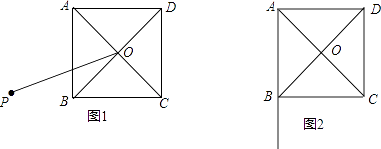
(2)点P在AB延长线上,且∠APO=30°,连接OP,以OP为一边,作正方形OPMN,且边ON与BC的延长线恰交于点N,连接CM,若AB=2,求CM的长(不必写出计算结果,简述求CM长的过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:8101×0.125100=
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)x2﹣6x+5=0
(2)2x2﹣3x﹣1=0.
相关试题

