【题目】如图,直线y=2x+3与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).

(1)求反比例函数的解析式;
(2)点D(a,1)是反比例函数y=![]() (x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=![]() ;(2)P(
;(2)P(![]() ,0).
,0).
【解析】
试题分析: (1)把x=1代入y=2x+3中,可求得B点坐标为(1,5),再带到反比例函数解析式中可求得反比例函数解析式;(2)作D关于x轴的对称点D′,连接BD′,与x轴交点即为点P.
试题解析:(1)∵BC⊥x轴于点C,且C点的坐标为(1,0),∴把x=1代入y=2x+3中,y=2+3=5,∴点B的坐标为(1,5),又∵点B(1,5)在反比例函数y=![]() 上,∴k=1×5=5,∴反比例函数的解析式为:y=
上,∴k=1×5=5,∴反比例函数的解析式为:y=![]() ;
;
(2)将点D(a,1)代入y=![]() ,得:a=5,∴点D坐标为(5,1),则点D(5,1)关于x轴的对称点为D′(5,﹣1),设过B(1,5)、D′(5,﹣1)的直线解析式为:y=kx+b,可得
,得:a=5,∴点D坐标为(5,1),则点D(5,1)关于x轴的对称点为D′(5,﹣1),设过B(1,5)、D′(5,﹣1)的直线解析式为:y=kx+b,可得![]() ,解得
,解得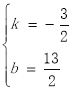 ,
,
∴直线BD′的解析式为:y=﹣![]() x+
x+![]() ,直线BD′与x轴的交点即为所求点P,当y=0时,得:﹣
,直线BD′与x轴的交点即为所求点P,当y=0时,得:﹣![]() x+
x+![]() =0,解得:x=
=0,解得:x=![]() ,故点P的坐标为(
,故点P的坐标为(![]() ,0).
,0).

-
科目: 来源: 题型:
查看答案和解析>>【题目】若一元二次方程x2﹣6x+m=0有两个相等的实数根,则m的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】因为直角三角形是特殊三角形,所以一般三角形全等的条件都可以用来说明2个直角三角形全等.________(判断对错)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,对称轴为直线x=
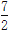 的抛物线经过点A(6,0)和B(0,﹣4).
的抛物线经过点A(6,0)和B(0,﹣4).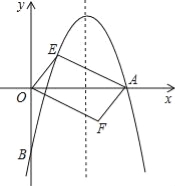
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第一象限,四边形OEAF是以OA为对角线的平行四边形,求平行四边形OEAF的面积S与x之间的函数关系式;
(3)当(2)中的平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形.
-
科目: 来源: 题型:
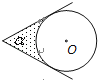
查看答案和解析>>【题目】如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )
A、
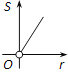 B、
B、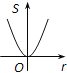 C、
C、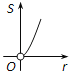 D、
D、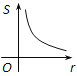
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,D是AC边上一点,E是BC延长线上一点,连接DE.
(1)如图1,若点D是AC中点,且DB=DE. 求证:AD=CE.
(2)如图2,若点D是AC边上任意一点,且DB=DE,则(1)中结论是否成立,如成立,请证明;如不成立,请说明理由.

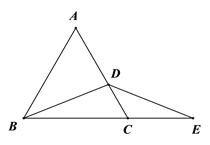
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD是矩形,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=4,DC=3,求BE的长.

相关试题

