【题目】如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD的平分线上时,则AE的长为( )

A. 2或3 B. ![]() 或
或![]() C.
C. ![]() 或
或![]() D. 3或4
D. 3或4
参考答案:
【答案】B
【解析】
如图,过点A1作A1M⊥BC于点M,A1N⊥AD于点N.设CM=A1M=x,则BM=7-x.在直角△A1MB中,由勾股定理得到:A1M2=A1B2-BM2=25-(7-x)2,由此求得x的值,进而得出AE的长.
如图,过点A1作A1M⊥BC于点M,A1N⊥AD于点N.

∵点A的对应点A1恰落在∠BCD的平分线上,
∴设CM=A1M=x,则BM=7x.
又由折叠的性质知AB=A1B=5.
∴在直角△A1MB中,由勾股定理得到:A1M2=A1B2BM2=25(7x)2.
∴25(7x)2=x2,
解得:x1=3,x2=4,
则A1N=ABA1M=2或1,
设AE=y,则A1E=y,EN=(4y)或(3y),
故y2=(4y)2+22,
解得:y=![]() ,
,
y2=(3y)2+12,
解得:y=![]()
故AE的长为![]() 或
或![]() .
.
故选:B
-
科目: 来源: 题型:
查看答案和解析>>【题目】拼图填空:剪裁出若干个大小.形状完全相同的直角三角形,三边长分别记为a.b.c,如图①.





(1)拼图一:分别用4张直角三角形纸片,拼成如图②③的形状,观察图②③可发现,图②中两个小正方形的面积之和 (填“大于”.“小于”或“等于”)图③中小正方形的面积,用关系式表示为 .
(2)拼图二:用4张直角三角形纸片拼成如图④的形状,观察图形可以发现,图中共有 个正方形,它们的面积之间的关系是 ,用关系式表示为 .
(3)拼图三:用8个直角三角形纸片拼成如图⑤的形状,图中3个正方形的面积之间的关系是 ,用关系式表示 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.

下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A. ① B. ② C. ①② D. ①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图7-①,图7-②,图7-③,图7-④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中的棋子个数是________,第
 个“广”字中的棋子个数是________
个“广”字中的棋子个数是________
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个命题:
(1)若点A在直线y=2x-3上,且点A到两坐标轴的距离相等,则点A在第一或第四象限;
(2)若A(a,m)、B(a-1,n)(a>0)在反比例函数y=
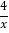
的图象上,则m<n;
(3)一次函数y=-2x-3的图象不经过第三象限;
(4)二次函数y=-2x2-8x+1的最大值是9.
正确命题的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①、②分别是某种型号跑步机的实物图与示意图.已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,求跑步机手柄的一端A的高度h(精确到0.1m).
(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)

-
科目: 来源: 题型:
查看答案和解析>>【题目】经过实验获得两个变量 x(x 0), y( y 0) 的一组对应值如下表。
x
1
2
3
4
5
6
7
y
7
3.5
2.33
1.75
1.4
1.17
1
(1)在网格中建立平面直角坐标系,画出相应的函数图象,求出这个函数表达式;
(2)结合函数图象解决问题:(结果保留一位小数)

①
 的值约为多少?
的值约为多少?②点A坐标为(6,0),点B在函数图象上,OA=OB,则点B的横坐标约是多少?
相关试题

