搜索
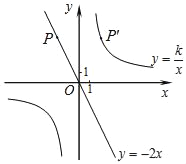
【题目】如图，已知直线y＝﹣2x经过点P（﹣2，a），点P关于y轴的对称点P′在反比例函数y＝
（k≠0）的图象上．
（1）求反比例函数的解析式；
（2）直接写出当y＜4时x的取值范围．
参考答案：
【答案】（1）y=
；（2）反比例函数自变量x的范围为x＞2或x＜0；一次函数自变量x的范围是x＞-2
【解析】
(1)把P的坐标代入直线的解析式，即可求得P的坐标，然后根据关于y轴对称的两个点之间的关系，即可求得P'的坐标，然后利用待定系数法即可求得反比例函数的解析式；
（2）根据反比例函数的增减性即可求得x的范围．
（1）把P（﹣2，a）代入直线y=-2x解析式得：a=4，即P（﹣2，4），
∴点P关于y轴对称点P′为（2，4），
代入反比例解析式得：k=8，
则反比例解析式为y=
；
（2）当y＜4时，反比例函数自变量x的范围为x＞2或x＜0；一次函数自变量x的范围是x＞-2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】两个反比例函数y=
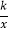（k＞1）和y=
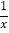在第一象限内的图象如图所示，点P在y=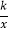的图象上，PC⊥x轴于点C，交y=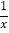的图象于点A，PD⊥y轴于点D，交y=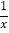的图象于点B，BE⊥x轴于点E，当点P在y=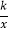图象上运动时，以下结论：①BA与DC始终平行；②PA与PB始终相等；③四边形PAOB的面积不会发生变化：④△OBA的面积等于四边形ACEB的面积．其中一定正确的是_____．（填序号）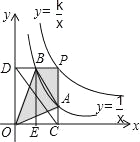
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知点A（10.0）及在第一象限的动点P（x,y），且x+y＝12，设△OPA的面积为S。
（1）求S关于x的函数解析式；
（2）求x的取值范围；
（3）当S＝15时，求P点坐标；
-
科目： 来源： 题型：
查看答案和解析>>【题目】某城市为了加强公民的节气和用气意识，按以下规定收取每月煤气费：所用煤气如果不超过50立方米，按每立方米0.8元收费；如果超过50立方米，超过部分按每立方米1.2元收费设小丽家每月所用煤气量为x立方米，应交煤气费为y元.
（1）若小丽家某月所用煤气量为80立方米，则小丽家该月应交煤气费多少元？
（2）试写出y与x之间的解析式.
（3）若小丽家4月份的煤气费为88元，则她家4月份所用煤气量为多少立方米？
（4）已知小丽家6月份所交的煤气费平均每立方米为0.95元，那么6月份小丽家用了多少立方米的煤气？
-
科目： 来源： 题型：
查看答案和解析>>【题目】一次函数y=kx+b与反比例函数y=
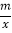的图象交于A（1，4），B（﹣2，n）两点．（1）求m和n的值；
（2）求k和b的值；
（3）结合图象直接写出不等式
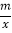-kx﹣b＞0的解集．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡，根据它们的质量（单位：
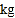），绘制出如下的统计图①和图②.请根据相关信息，解答下列问题：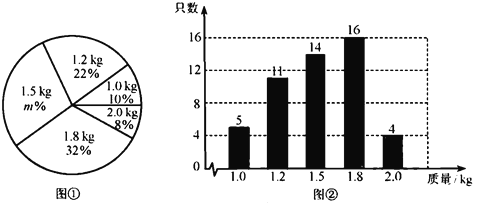
（Ⅰ）图①中
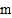的值为 ；（Ⅱ）求统计的这组数据的平均数、众数和中位数；
（Ⅲ） 根据样本数据，估计这2500只鸡中，质量为
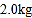的约有多少只？ -
科目： 来源： 题型：
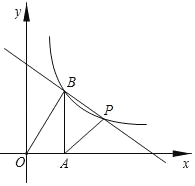
查看答案和解析>>【题目】如图，在平面直角坐标系中，函数y=
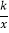的图象经过点P（4，3）和点B（m，n）（其中0＜m＜4），作BA⊥x轴于点A，连接PA，PB，OB，已知S△AOB=S△PAB．（1）求k的值和点B的坐标．
（2）求直线BP的解析式．
（3）直接写出在第一象限内，使反比例函数大于一次函数的x的取值范围是 ．
相关试题
