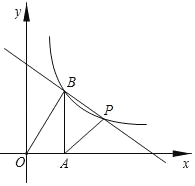
【题目】如图,在平面直角坐标系中,函数y=![]() 的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA,PB,OB,已知S△AOB=S△PAB.
的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA,PB,OB,已知S△AOB=S△PAB.
(1)求k的值和点B的坐标.
(2)求直线BP的解析式.
(3)直接写出在第一象限内,使反比例函数大于一次函数的x的取值范围是 .
参考答案:
【答案】(1)k=12;B(2,6);(2)y=﹣![]() x+9;(3)0<x<2或x>4.
x+9;(3)0<x<2或x>4.
【解析】
(1)把P(4,3)代入y=![]() ,即可求出k的值;由S△AOB=S△PAB可求出点B的横坐标,代入反比例函数解析式可求出点B的坐标;
,即可求出k的值;由S△AOB=S△PAB可求出点B的横坐标,代入反比例函数解析式可求出点B的坐标;
(2)设直线BP的解析式为y=ax+b,将B(2,6),P(4,3)代入,利用待定系数法即可求出直线BP的解析式;
(3)根据图像直接写出结论即可.
(1)将P(4,3)代入函数y=![]() ,得:k=4×3=12,
,得:k=4×3=12,
∴反比例函数为y=![]() ,
,
∵△AOB和△PAB都可以看作以AB为底,它们的面积相等,
∴它们的底AB边上的高也相等,即点O和点P到直线AB的距离相等,
∴xP=2xB,
∵P(4,3),即xP=4,
∴xB=2,
代入y=![]() ,得:y=6,
,得:y=6,
∴B(2,6);
(2)设直线BP的解析式为y=ax+b,
分别代入B(2,6)、P(4,3),
得:![]() ,
,
解得![]() ,
,
∴直线BP的解析式为y=﹣![]() x+9;
x+9;
(3)在第一象限内,反比例函数大于一次函数的x的取值范围是0<x<2或x>4,
故答案为:0<x<2或x>4.
-
科目: 来源: 题型:
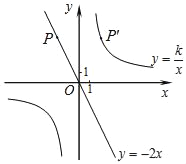
查看答案和解析>>【题目】如图,已知直线y=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数y=
 (k≠0)的图象上.
(k≠0)的图象上.(1)求反比例函数的解析式;
(2)直接写出当y<4时x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b与反比例函数y=
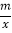 的图象交于A(1,4),B(﹣2,n)两点.
的图象交于A(1,4),B(﹣2,n)两点.(1)求m和n的值;
(2)求k和b的值;
(3)结合图象直接写出不等式
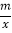 -kx﹣b>0的解集.
-kx﹣b>0的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位:
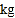 ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题: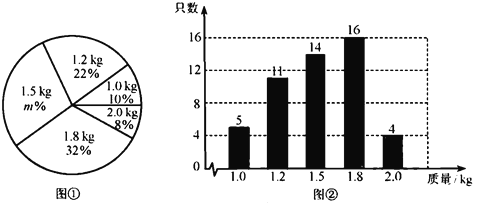
(Ⅰ)图①中
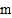 的值为 ;
的值为 ;(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ) 根据样本数据,估计这2500只鸡中,质量为
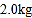 的约有多少只?
的约有多少只? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为选拔一名选手参加“美丽邵阳,我为家乡做代言”主题演讲比赛,经研究,按图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整).下表是李明、张华在选拔赛中的得分情况:
项目
选手
服装
普通话
主题
演讲技巧
李明
85
70
80
85
张华
90
75
75
80
结合以上信息,回答下列问题:
(1)求服装项目的权数及普通话项目对应扇形的圆心角大小;
(2)求李明在选拔赛中四个项目所得分数的众数和中位数;
(3)根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽邵阳,我为家乡做代言”主题演讲比赛,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】绵阳某公司销售统计了每个销售员在某月的销售额,绘制了如下折线统计图和扇形统计图:
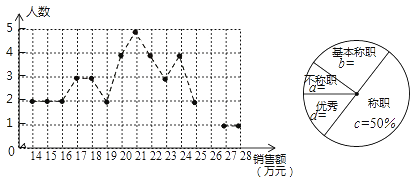
设销售员的月销售额为x(单位:万元)。销售部规定:当x<16时,为“不称职”,当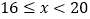 时为“基本称职”,当
时为“基本称职”,当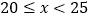 时为“称职”,当
时为“称职”,当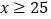 时为“优秀”.根据以上信息,解答下列问题:
时为“优秀”.根据以上信息,解答下列问题: (1)补全折线统计图和扇形统计图;
(2)求所有“称职”和“优秀”的销售员销售额的中位数和众数;
(3)为了调动销售员的积极性,销售部决定制定一个月销售额奖励标准,凡月销售额达到或超过这个标准的销售员将获得奖励。如果要使得所有“称职”和“优秀”的销售员的一半人员能获奖,月销售额奖励标准应定为多少万元(结果去整数)?并简述其理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,面积为4的正方形OABC的顶点O与坐标原点重合,边OA、OC分别在x轴、y轴的正半轴上,点B、P都在函数y=
 (x>0)的图象上,过动点P分别作轴x、y轴的平行线,交y轴、x轴于点D、E.设矩形PDOE与正方形OABC重叠部分图形的面积为S,点P的横坐标为m.
(x>0)的图象上,过动点P分别作轴x、y轴的平行线,交y轴、x轴于点D、E.设矩形PDOE与正方形OABC重叠部分图形的面积为S,点P的横坐标为m.(1)求k的值;
(2)用含m的代数式表示CD的长;
(3)求S与m之间的函数关系式.

相关试题

