【题目】两个反比例函数y=![]() (k>1)和y=
(k>1)和y=![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y=![]() 的图象上,PC⊥x轴于点C,交y=
的图象上,PC⊥x轴于点C,交y=![]() 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y=![]() 的图象于点B,BE⊥x轴于点E,当点P在y=
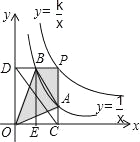
的图象于点B,BE⊥x轴于点E,当点P在y=![]() 图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化:④△OBA的面积等于四边形ACEB的面积.其中一定正确的是_____.(填序号)
图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化:④△OBA的面积等于四边形ACEB的面积.其中一定正确的是_____.(填序号)
参考答案:
【答案】①③④
【解析】
设出点P的坐标,由此可得出A、C、B、D点的坐标,由点的坐标即可表示出各线段的长度,根据线段间的比例关系即可得出BA∥DC,即①成立;找出当PA=PB时,m的值,由此发现②不一定成立;③根据反比例函数系数k的几何意义可得出三角形OBD、OAC以及矩形OCPD的面积,分割图形即可得出S四边形PAOB=k-1,即③成立;根据各边长度计算出S梯形BECA,结合三角形的面积公式求出S△OBA,发现二者相等,由此得知④成立.综上即可得出结论.
解:如图,
①正确.∵A、B在y=![]() 上,
上,
∴S△AOC=S△BOE,
∴![]() OCAC=
OCAC=![]() OEBE,
OEBE,
∴OCAC=OEBE,
∵OC=PD,BE=PC,
∴PDAC=DBPC,
∴![]() ,
,
∴AB∥CD.故此选项正确.
②错误,不一定,只有当四边形OCPD为正方形时满足PA=PB;
③正确,由于矩形OCPD、△ODB、△OCA的面积为定值,则四边形PAOB的面积不会发生变化;故此选项正确.
④正确.∵△ODB的面积=△OCA的面积=![]() ,
,
∴△ODB与△OCA的面积相等,同理可得:S△ODB=S△OBE,
∵△OBA的面积=矩形OCPD的面积﹣S△ODB﹣S△BAP﹣S△AOC,四边形ACEB的面积=矩形OCPD的面积﹣S△ODB﹣S△BAP﹣S△OBE
∴△OBA的面积=四边形ACEB的面积,故此选项正确,
故一定正确的是①③④.
故答案为:①③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于一次函数y=﹣2x+3,下列结论正确的是( )
A. 图象过点(1,﹣1) B. 图象经过一、二、三象限
C. y随x的增大而增大 D. 当x>
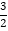 时,y<0
时,y<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列不是一次函数关系的是( )
A.矩形一条边的长固定,面积与另一条边的长的关系
B.矩形一条边的长固定,周长与另一条边的长的关系
C.圆的周长与直径的关系
D.圆的面积与直径的关系
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 的解析式为
的解析式为 ,它与坐标轴分别交于A,B两点.
,它与坐标轴分别交于A,B两点.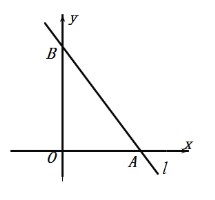
(1)求出点A的坐标;
(2)动点C从y轴上的点
 出发,以每秒1个单位长度的速度向y轴负半轴运动,求出点C运动的时间t,使得
出发,以每秒1个单位长度的速度向y轴负半轴运动,求出点C运动的时间t,使得 为等腰三角形.
为等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(10.0)及在第一象限的动点P(x,y),且x+y=12,设△OPA的面积为S。
(1)求S关于x的函数解析式;
(2)求x的取值范围;
(3)当S=15时,求P点坐标;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市为了加强公民的节气和用气意识,按以下规定收取每月煤气费:所用煤气如果不超过50立方米,按每立方米0.8元收费;如果超过50立方米,超过部分按每立方米1.2元收费设小丽家每月所用煤气量为x立方米,应交煤气费为y元.
(1)若小丽家某月所用煤气量为80立方米,则小丽家该月应交煤气费多少元?
(2)试写出y与x之间的解析式.
(3)若小丽家4月份的煤气费为88元,则她家4月份所用煤气量为多少立方米?
(4)已知小丽家6月份所交的煤气费平均每立方米为0.95元,那么6月份小丽家用了多少立方米的煤气?
-
科目: 来源: 题型:
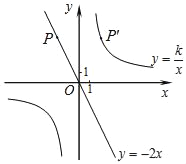
查看答案和解析>>【题目】如图,已知直线y=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数y=
 (k≠0)的图象上.
(k≠0)的图象上.(1)求反比例函数的解析式;
(2)直接写出当y<4时x的取值范围.
相关试题

