【题目】为了更好治理西太湖水质,保护环境,市治污公司决定购买10 台污水处理设备,现有A、B两种型号的设备,其中每台的价格,月处理污水量如下表:

经调查:购买-台A型设备比购买一-台B型设备多2万元,购买2台A型设备比购买4台B型设备少4万元.
(1)求a、b的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过47万元,并且该月要求处理西太湖的污水量不低于1860 吨,则有哪几种购买方案?请指出最省钱的一种购买方案,并指出相应的费用.
参考答案:
【答案】(1) ![]() ; (2) 购买方案:①A型设备1台,B型设备9台:②A型设备2台,B型设备8台;
; (2) 购买方案:①A型设备1台,B型设备9台:②A型设备2台,B型设备8台;
③A型设备3台,B型设备7台,最省钱的购买方案:选购A型设备1台,B型设备9台,费用42万.
【解析】
(1) 购买A型的价格是a万元,购买B型的设备b万元,根据购买一-台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买4台B型设备少4万元可列方程组求解;
(2)设购买A型号设备x台,则B型为(0-x)台,根据使治污公司购买污水处理设备的资金不超过47万元,利用每月要求处理污水量不低于1860 吨,可列不等式组求解.
(1) 根据题意得:![]() ,
,
解得: ![]() ;
;
(2)设购买污水处理设备A型设备x台,B型设备![]() 台,
台,
根据题意得,![]() ,
,
解得:![]() ,
,
∴x为1、2,3.
购买方案:①A型设备1台,B型设备9台;
②A型设备2台,B型设备8台;
③A型设备3台,B型设备7台;
∴为了节约资金,应选购A型设备1台,B型设备9台,其费用=![]() 万.
万.
-
科目: 来源: 题型:
查看答案和解析>>【题目】李师傅负责修理我校课桌椅,现知道李师傅修理2张课桌和3把椅子共需86分钟,修理5张课桌和2把椅子共需149分钟.
(1)请问李师傅修理1张课桌和1把椅子各需多少分钟
(2)现我校有12张课桌和14把椅子需要修理,要求1天做完,李师傅每天工作8小时,请问李师傅能在上班时间内修完吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1,
①b2>4ac;②4a﹣2b+c<0;③不等式ax2+bx+c>0的解集是x>3;④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2 .
上述判断中,正确的是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.
利用数形结合思想回答下列问题:
(1)数轴上表示1和3两点之间的距离 .
(2)数轴上表示﹣12和﹣6的两点之间的距离是 .
(3)数轴上表示x和1的两点之间的距离表示为 .
(4)若x表示一个有理数,且﹣4<x<2,则|x﹣2|+|x+4|= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(注:结果保留π )
(1)把圆片沿数轴向右滚动半周,点B到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 ;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 ;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3.
①第 次滚动后,A点距离原点最近,第 次滚动后,A点距离原点最远.
②当圆片结束运动时,A点运动的路程共有 ,此时点A所表示的数是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(1)点P(-1,6)的“2属派生点”P′的坐标为_____________;
(2)若点P的“3属派生点”P′的坐标为(6,2),则点P的坐标___________;
(3)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
-
科目: 来源: 题型:
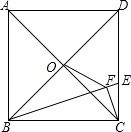
查看答案和解析>>【题目】如图,正方形ABCD的边长为3,点0是对角线AC,BD的交点,点E在CD上,且DE=2CE,连接BE.过点C作CF⊥BE,垂足为F,连接OF,则OF的长为 .
相关试题

