【题目】如图,正方形![]() 和正方形
和正方形![]() 中,点
中,点![]() 在CG上,BC=1,CE=3,H是AF的中点,那么
在CG上,BC=1,CE=3,H是AF的中点,那么![]() 的长是( )
的长是( )

A.![]() B.
B.![]() C.
C.![]() D.2
D.2
参考答案:
【答案】B
【解析】
延长BA和FG交于点M,连接AC和CF,根据正方形的性质可得四边形MADG为矩形,GM=AB=BC=CD=1, GC=CE=GF=3,∠ACD=∠GCF=45°,从而求出MA、MF、∠M和∠ACF,根据勾股定理即可求出AF,然后根据直角三角形斜边上的中线等于斜边的一半即可求出结论.
解:延长BA和FG交于点M,连接AC和CF

∵正方形![]() 和正方形
和正方形![]() 中,BC=1,CE=3,
中,BC=1,CE=3,
∴四边形MADG为矩形,GM=AB=BC=CD=1, GC=CE=GF=3,∠ACD=∠GCF=45°
∴MA=GD=GC-CD=2,MF=GM+GF=4,∠M=90°,∠ACF=∠ACD+∠GCF=90°
根据勾股定理可得AF=![]()
∵H是AF的中点,
∴CH=![]() AF=
AF=![]()
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高农民收入,某区一水果公园引进一种新型蟠桃,蟠桃进价为每公斤40元.上市后通过一段时间的试营销发现:当蟠桃销售单价在每公斤40元至90元之间(含40元和90元)时,每月的销售量
 (公斤)与销售单价
(公斤)与销售单价 (元/公斤)之间的关系可近似地看作一次函数,其图像如图所示.
(元/公斤)之间的关系可近似地看作一次函数,其图像如图所示.(1)求
 与
与 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;(2)如果想要每月获得2400元的利润,那么销售单价应定为每公斤多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数
 的图像与反比例函数
的图像与反比例函数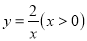 的图像相交于点
的图像相交于点 ,一次函数
,一次函数 与
与 轴相交于点
轴相交于点 ,与
,与 轴相交于点
轴相交于点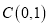 .
.(1)求
 和
和 的值;
的值;(2)点
 在
在 轴正半轴上,且
轴正半轴上,且 的面积为1,求点
的面积为1,求点 坐标;
坐标;(3)在(2)的条件下,点
 是一次函数
是一次函数 上一点,点
上一点,点 是反比例函数
是反比例函数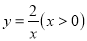 图像上一点,且点
图像上一点,且点 、
、 都在
都在 轴上方.如果以
轴上方.如果以 、
、 、
、 、
、 为顶点的四边形为平行四边形,请直接写出点
为顶点的四边形为平行四边形,请直接写出点 、
、 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,对角线AC,BD相交于点O,不添加任何辅助线,要使四边形ABCD是正方形,则需要添加一个条件是 . (填一个即可)

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明正在做一个半径为
 米的地球模型.
米的地球模型.(1)他想用一根铁丝围住地球模型的赤道,大约需要多少的铁丝?如果要把这个模型的半径增加
 米,要围住赤道需要增加多长的铁丝?
米,要围住赤道需要增加多长的铁丝?(2)假设真的为地球赤道做一个铁箍,大约要多长的铁丝?如果将铁箍所围的半径增加
 米,那么需要增加多长的铁丝?(地球半径约为
米,那么需要增加多长的铁丝?(地球半径约为 千米)
千米)(3)比较(1)(2)的结果,请叙述一下你发现了什么?
(4)如果小明做的地球的模型的半径为
 ,如果地球体积是地球模型体积的
,如果地球体积是地球模型体积的 倍,求
倍,求 的值.(球的体积公式
的值.(球的体积公式 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AC、BD交于点O,BD⊥AD于点D,将△ABD沿BD翻折得到△EBD,连接EC、EB.
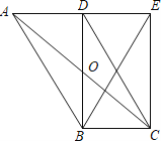
(1)求证:四边形DBCE是矩形;
(2)若BD=4,AD=3,求点O到AB的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形BEDG和矩形BNDQ中,BE=BN,DE=DN.
(1)将两个矩形叠合成如图10,求证:四边形ABCD是菱形;
(2)若菱形ABCD的周长为20,BE=3,求矩形BEDG的面积.

相关试题

