【题目】某中学了解本校学生对球类运动的爱好情况,分为足球、篮球、排球、其他四个方面调查若干名学生,每人只选其中之一,统计后绘制成不完整的“折线统计图”(扇形统计图),根据信息解答下列问题: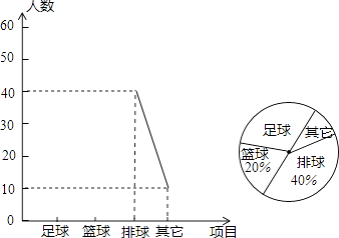
(1)在这次调查中,一共调查名学生;
(2)在扇形统计图中,“足球”所在扇形圆心角度;
(3)将折线统计图补充完整.
参考答案:
【答案】
(1)100
(2)108
(3)解:爱好“足球”人数为:100×30%=30人,
爱好“篮球”人数为:100﹣30﹣40﹣10=20人,补全折线统计图如下:
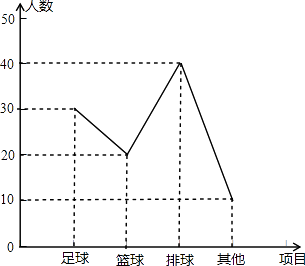
【解析】解:(1)根据题意,知爱好“排球”的有40人,占被调查人数的40%,
故被调查人数为:40÷40%=100(人);(2)“其他”项目占被调查人数百分比为: ![]() ×100%=10%,则“足球”项目人数占被调查人数的百分比为:1﹣(20%+40%+10%)=30%,
×100%=10%,则“足球”项目人数占被调查人数的百分比为:1﹣(20%+40%+10%)=30%,
则在扇形统计图中,“足球”所在扇形圆心角为:360°×30%=108°;
所以答案是:(1)100,(2)108.
【考点精析】关于本题考查的扇形统计图和折线统计图,需要了解能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地反映事物的变化情况,但是不能清楚地表示出在总体中所占的百分比才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“低碳环保、绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以
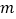 米/分的速度到达图书馆.小军始终以同一速度骑行,两人行驶的路程
米/分的速度到达图书馆.小军始终以同一速度骑行,两人行驶的路程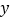 (米)与时间
(米)与时间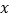 (分钟)的关系如图.请结合图象,解答下列问题:
(分钟)的关系如图.请结合图象,解答下列问题:(1)
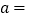 ;
;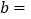 ;
;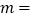 ;
;(2)若小军的速度是120米/分,求小军在图中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
(4)若小军的行驶速度是
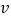 米/分,且在图中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出
米/分,且在图中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出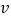 的取值范围.
的取值范围.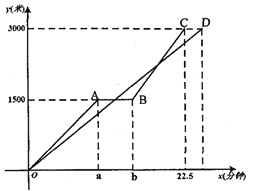
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 于
于 ,
, ,
, ,
, ,
, 分别是
分别是 ,
, 的中点.
的中点.
(1)求证:
 ,
,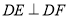 ;
;(2)连接
 ,若
,若 ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据:21,23,25,25,26,这组数据的平均数和中位数分别是( )
A.24,25B.24,24C.25,24D.25,25
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中:正确的说法有
①两个全等三角形合在一起是一个轴对称图形;
②成轴对称的两个图形一定全等;
③直线l经过线段AB的中点,则l是线段AB的垂直平分线;
④一条线段可以看作是以它的垂直平分线为对称轴的轴对称图形.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, 为
为 边上一点,
边上一点, 平分
平分 ,
, 为
为 的中点,连接
的中点,连接 ,过点
,过点 作
作 分别交
分别交 于
于 ,
, 两点.
两点. 
(1)求证:
 ;
;(2)求证:
 ;
;(3)当
 时,请直接写出
时,请直接写出 的长.
的长.
相关试题

