【题目】如图,在![]() 中,
中,![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.

(1)求证:![]() ,
,![]() ;
;
(2)连接![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1)证明见解析;(2)EF=5![]() .
.
【解析】
试题分析:(1)证明△BDG≌△ADC,根据全等三角形的性质、直角三角形的性质证明;
(2)根据直角三角形的性质分别求出DE、DF,根据勾股定理计算即可.
试题解析:(1)∵AD⊥BC,∴∠ADB=∠ADC=90°,在△BDG和△ADC中, ,
,
∴△BDG≌△ADC,∴BG=AC,∠BGD=∠C,
∵∠ADB=∠ADC=90°,E,F分别是BG,AC的中点,∴DE=![]() BG=EG,DF=
BG=EG,DF=![]() AC=AF,
AC=AF,
∴DE=DF,∠EDG=∠EGD,∠FDA=∠FAD,∴∠EDG+∠FDA=90°,∴DE⊥DF;
(2)∵AC=10,∴DE=DF=5,由勾股定理得,EF=![]() =5
=5![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在线段、圆、角、正三角形、平行四边形、矩形中,是轴对称的图形有( )
A. 3个 B. 4个 C. 5个 D. 6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】由a>b,得到ma<mb,则m的取值范围是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“低碳环保、绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以
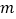 米/分的速度到达图书馆.小军始终以同一速度骑行,两人行驶的路程
米/分的速度到达图书馆.小军始终以同一速度骑行,两人行驶的路程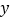 (米)与时间
(米)与时间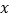 (分钟)的关系如图.请结合图象,解答下列问题:
(分钟)的关系如图.请结合图象,解答下列问题:(1)
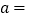 ;
;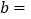 ;
;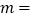 ;
;(2)若小军的速度是120米/分,求小军在图中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
(4)若小军的行驶速度是
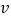 米/分,且在图中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出
米/分,且在图中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出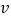 的取值范围.
的取值范围.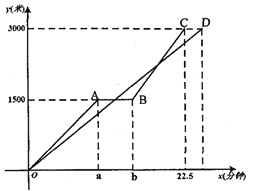
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据:21,23,25,25,26,这组数据的平均数和中位数分别是( )
A.24,25B.24,24C.25,24D.25,25
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学了解本校学生对球类运动的爱好情况,分为足球、篮球、排球、其他四个方面调查若干名学生,每人只选其中之一,统计后绘制成不完整的“折线统计图”(扇形统计图),根据信息解答下列问题:
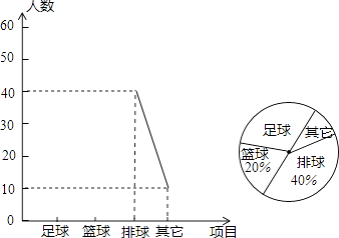
(1)在这次调查中,一共调查名学生;
(2)在扇形统计图中,“足球”所在扇形圆心角度;
(3)将折线统计图补充完整. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中:正确的说法有
①两个全等三角形合在一起是一个轴对称图形;
②成轴对称的两个图形一定全等;
③直线l经过线段AB的中点,则l是线段AB的垂直平分线;
④一条线段可以看作是以它的垂直平分线为对称轴的轴对称图形.
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

