【题目】如图,在矩形![]() 中,
中,![]() 为
为![]() 边上一点,
边上一点,![]() 平分
平分![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,过点
,过点![]() 作
作![]() 分别交
分别交![]() 于
于![]() ,
,![]() 两点.
两点.

(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)当![]() 时,请直接写出
时,请直接写出![]() 的长.
的长.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)4![]() .
.
【解析】
试题分析:(1)根据平行线的性质以及角平分线的定义,即可得到∠DCE=∠DEC,进而得出DE=DC;
(2)连接DF,根据等腰三角形的性质得出∠DFC=90°,再根据直角三角形斜边上中线的性质得出BF=CF=EF=![]() EC,再根据SAS判定△ABF≌△DCF,即可得出∠AFB=∠DFC=90°,据此可得AF⊥BF;
EC,再根据SAS判定△ABF≌△DCF,即可得出∠AFB=∠DFC=90°,据此可得AF⊥BF;
(3)根据等角的余角相等可得∠BAF=∠FEH,再根据公共角∠EFG=∠AFE,即可判定△EFG∽△AFE,进而得出EF2=AFGF=28,求得EF=2![]() ,即可得到CE=2EF=4
,即可得到CE=2EF=4![]() .
.
试题解析:(1)∵四边形ABCD是矩形,∴AB∥CD,∴∠DCE=∠CEB,
∵EC平分∠DEB,∴∠DEC=∠CEB,∴∠DCE=∠DEC,∴DE=DC;
(2)如图,连接DF,
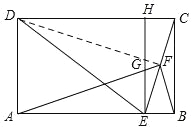
∵DE=DC,F为CE的中点,∴DF⊥EC,∴∠DFC=90°,
在矩形ABCD中,AB=DC,∠ABC=90°,∴BF=CF=EF=![]() EC,∴∠ABF=∠CEB,
EC,∴∠ABF=∠CEB,
∵∠DCE=∠CEB,∴∠ABF=∠DCF,
在△ABF和△DCF中,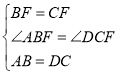 ,∴△ABF≌△DCF(SAS),∴∠AFB=∠DFC=90°,
,∴△ABF≌△DCF(SAS),∴∠AFB=∠DFC=90°,
∴AF⊥BF;
(3)CE=4![]() .
.
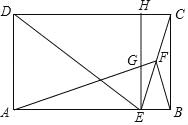
理由如下:∵AF⊥BF,∴∠BAF+∠ABF=90°,
∵EH∥BC,∠ABC=90°,∴∠BEH=90°,∴∠FEH+∠CEB=90°,
∵∠ABF=∠CEB,∴∠BAF=∠FEH,
∵∠EFG=∠AFE,∴△EFG∽△AFE,∴![]() ,即EF2=AFGF,
,即EF2=AFGF,
∵AFGF=28,∴EF=2![]() ,∴CE=2EF=4
,∴CE=2EF=4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学了解本校学生对球类运动的爱好情况,分为足球、篮球、排球、其他四个方面调查若干名学生,每人只选其中之一,统计后绘制成不完整的“折线统计图”(扇形统计图),根据信息解答下列问题:
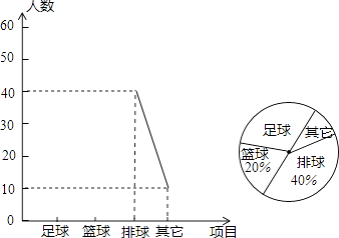
(1)在这次调查中,一共调查名学生;
(2)在扇形统计图中,“足球”所在扇形圆心角度;
(3)将折线统计图补充完整. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中:正确的说法有
①两个全等三角形合在一起是一个轴对称图形;
②成轴对称的两个图形一定全等;
③直线l经过线段AB的中点,则l是线段AB的垂直平分线;
④一条线段可以看作是以它的垂直平分线为对称轴的轴对称图形.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据不等式的基本性质,以下各题的结论正确的是( )
A.若a≥b,则5b≤5aB.若b﹣3a>0,则b<3a
C.若﹣5x≥20,则x≥﹣4D.若a≤b,则ac≤bc
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,是轴对称图形但不是中心对称图形的是( )
A.圆B.等腰三角形C.平行四边形D.菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】将命题“正方形的四条边都相等”改为“如果…那么…”的形式为_____.
相关试题

