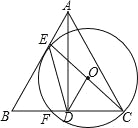
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,E为边AB上一点,ED=CD,以CE为直径作⊙O,交BC于点F.
(1)求证:AB与⊙O相切;
(2)若DF=1,DC=3,求AE的长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)根据等腰三角形的性质,由AB=AC,AD⊥BC得到BD=CD,则可判断OD为△BCE的中位线,所以OD∥BE,再根据等腰三角形的性质,由DE=DC,OE=OC得到DO⊥CE,则BE⊥CE,于是根据切线的性质可判断AB与⊙O相切;
(2)连结EF,如图,根据圆周角定理得∠EFC=90°,在Rt△DEF中利用勾股定理计算出EF=2![]() ,再在Rt△BEF中利用勾股定理计算出BE=2
,再在Rt△BEF中利用勾股定理计算出BE=2![]() ,然后根据平行线分线段成比例定理可求出AE的长.
,然后根据平行线分线段成比例定理可求出AE的长.
试题解析:(1)∵AB=AC,AD⊥BC,
∴BD=CD,
∵OE=OC,
∴OD为△BCE的中位线,
∴OD∥BE,
∵DE=DC,OE=OC,
∴DO⊥CE,
∴BE⊥CE,
∴AB与⊙O相切;
(2)连结EF,如图,
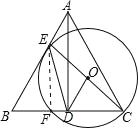
∵CE为⊙O的直径,
∴∠EFC=90°,
在Rt△DEF中,∵DE=DC=3,DF=1,
∴EF=![]() ,
,
∵DB=DC=3,
∴BF=BD-DF=3-1=2,
在Rt△BEF中,∵EF=2![]() ,BF=2,
,BF=2,
∴BE=![]() ,
,
∵EF∥AD,
∴![]() ,即
,即![]() ,
,
∴AE=![]() .
.
-
科目: 来源: 题型:
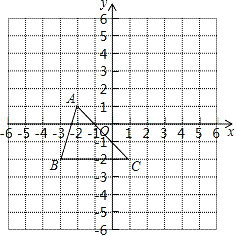
查看答案和解析>>【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1.
(1)在图中画出△A1B1C1;
(2)点A1,B1,C1的坐标分别为 、 、 ;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a3﹣a2=a B. a2a3=a6 C. a6÷a2=a3 D. (a2)3=a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a2+a2=a4B. 3(a﹣b)=3a﹣b
C. (﹣b2)3=﹣b5D. a2a2=a4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(a>0)的顶点为(2,4),若点(﹣2,m),(3,n)在抛物线上,则m_____n(填“>”、“=”或“<”).
-
科目: 来源: 题型:
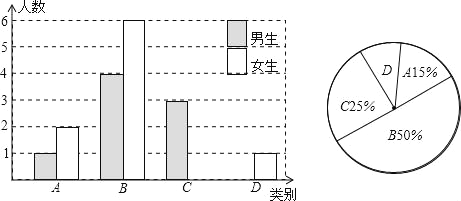
查看答案和解析>>【题目】随着科技的不断发展,人与人的沟通方式也发生了很大的变化,广州市某中学九年级的一个数学兴趣小组在本年级学生中进行“学生最常用的交流方式”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为四类:A.面对面交谈;B.微信和QQ等聊天软件交流;C.短信与书信交流;D.电话交流.根据调查数据结果绘制成以下两幅不完整的统计图
(1)本次调查,一共调查了 名同学,其中C类女生有 名,D类男生有 名;
(2)若该年级有学生150名,请根据调查结果估计这些学生中以“D.电话交流”为最常用的交流方式的人数约为多少?
(3)在本次调查中以“C.短信与书信交流”为最常用交流方式的几位同学中随机抽取两名同学参加广州市中学生书信节比赛,请用列举法求所抽取的两名同学都是男同学的概率.
-
科目: 来源: 题型:
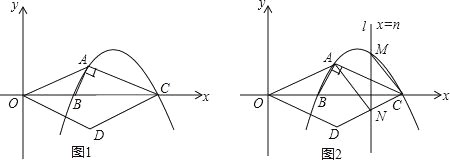
查看答案和解析>>【题目】如图1,抛物线y=ax2-11ax+24a(a<0)与x轴交于B、C两点(点B在点C的左侧),抛物线上另有一点A在第一象限内,且∠BAC=90°.
(1)求线段OC的长和点B的坐标;
(2)连接OA,将△OAC沿x轴翻折后得△ODC,当四边形OACD是菱形时,求此时抛物线的解析式;
(3)如图2,折垂直于x轴的直线l:x=n与(2)中所求的抛物线交于点M,与CD交于点N,若直线l沿x轴方向左右平移,且交点M始终位于抛物线上A、C两点之间时,试探究:当n为何值时,四边形AMCN的面积取得最大值,并求这个最大值;
(4)在(3)的条件下,当取得最大值时,四边形ADNM是否为平行四边形?直接回答 (是或不是).如果不是,请直接写出此时的点M的坐标.
相关试题

