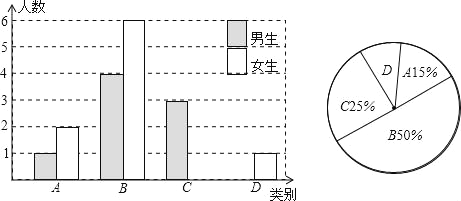
【题目】随着科技的不断发展,人与人的沟通方式也发生了很大的变化,广州市某中学九年级的一个数学兴趣小组在本年级学生中进行“学生最常用的交流方式”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为四类:A.面对面交谈;B.微信和QQ等聊天软件交流;C.短信与书信交流;D.电话交流.根据调查数据结果绘制成以下两幅不完整的统计图
(1)本次调查,一共调查了 名同学,其中C类女生有 名,D类男生有 名;
(2)若该年级有学生150名,请根据调查结果估计这些学生中以“D.电话交流”为最常用的交流方式的人数约为多少?
(3)在本次调查中以“C.短信与书信交流”为最常用交流方式的几位同学中随机抽取两名同学参加广州市中学生书信节比赛,请用列举法求所抽取的两名同学都是男同学的概率.
参考答案:
【答案】(1)20,2,1;(2)15名;(3)![]() .
.
【解析】
试题分析:(1)由题意可求得本次调查,一共调查了:(4+6)÷50%=20(名);继而求得C类总人数,继而求得C类女生数,然后求得D类男生数;
(2)由(1)中以“D.电话交流”为最常用的交流方式的占:1-15%-25%-50%=10%,即可求得答案;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所抽取的两名同学都是男同学的情况,再利用概率公式即可求得答案.
试题解析:(1)本次调查,一共调查了:(4+6)÷50%=20(名);
∵其中C类共有:20×25%=5(名),
∴C类女生有:5-3=2(名);
∴D类男生共有20-1-2-4-6-5-1=1(名);
(2)∵以“D.电话交流”为最常用的交流方式的占:1-15%-25%-50%=10%,
∴150×10%=15(名),
∴估计这些学生中以“D.电话交流”为最常用的交流方式的人数约为15名;
(3)画树状图得:
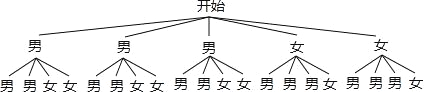
∵共有20种等可能的结果,所抽取的两名同学都是男同学的有6种情况,
∴所抽取的两名同学都是男同学的概率为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a2+a2=a4B. 3(a﹣b)=3a﹣b
C. (﹣b2)3=﹣b5D. a2a2=a4
-
科目: 来源: 题型:
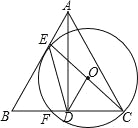
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,E为边AB上一点,ED=CD,以CE为直径作⊙O,交BC于点F.
(1)求证:AB与⊙O相切;
(2)若DF=1,DC=3,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(a>0)的顶点为(2,4),若点(﹣2,m),(3,n)在抛物线上,则m_____n(填“>”、“=”或“<”).
-
科目: 来源: 题型:
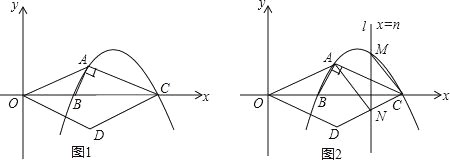
查看答案和解析>>【题目】如图1,抛物线y=ax2-11ax+24a(a<0)与x轴交于B、C两点(点B在点C的左侧),抛物线上另有一点A在第一象限内,且∠BAC=90°.
(1)求线段OC的长和点B的坐标;
(2)连接OA,将△OAC沿x轴翻折后得△ODC,当四边形OACD是菱形时,求此时抛物线的解析式;
(3)如图2,折垂直于x轴的直线l:x=n与(2)中所求的抛物线交于点M,与CD交于点N,若直线l沿x轴方向左右平移,且交点M始终位于抛物线上A、C两点之间时,试探究:当n为何值时,四边形AMCN的面积取得最大值,并求这个最大值;
(4)在(3)的条件下,当取得最大值时,四边形ADNM是否为平行四边形?直接回答 (是或不是).如果不是,请直接写出此时的点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场在销售旺季临近时,某品牌的童装销售价格呈上升趋势,假如这种童装开始时的售价为每件20元,并且每周(7天)涨价2元,从第6周开始,保持每件30元的稳定价格销售,直到11周结束,该童装不再销售.
(1)请建立销售价格y(元)与周次x之间的函数关系;
(2)若该品牌童装于进货当周售完,且这种童装每件进价z(元)与周次x之间的关系为z=-
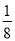 (x-8)2+12,1≤x≤11,且x为整数,那么该品牌童装在第几周售出后,每件获得利润最大?并求最大利润为多少?
(x-8)2+12,1≤x≤11,且x为整数,那么该品牌童装在第几周售出后,每件获得利润最大?并求最大利润为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】点A和点B(2,-3)关于x轴对称,则A、B两点间的距离为( )
A.4
B.5
C.6
D.10
相关试题

