【题目】在研究相似问题时,甲、乙同学的观点如下: 甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )
A.两人都对
B.两人都不对
C.甲对,乙不对
D.甲不对,乙对
参考答案:
【答案】A
【解析】解:甲:根据题意得:AB∥A′B′,AC∥A′C′,BC∥B′C′, ∴∠A=∠A′,∠B=∠B′,
∴△ABC∽△A′B′C′,
∴甲说法正确;
乙:∵根据题意得:AB=CD=3,AD=BC=5,则A′B′=C′D′=3+2=5,A′D′=B′C′=5+2=7,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴新矩形与原矩形不相似.
∴乙说法正确.
故选:A.
【考点精析】本题主要考查了相似三角形的判定的相关知识点,需要掌握相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,AE为⊙O的切线,若tan∠ABE=
 ,AE=3,求BD的长.
,AE=3,求BD的长. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠ABC=60°,对角线AC、BD相交于点O,将对角线AC所在的直线绕点O顺时针旋转角α(0°<α<90°)后得直线l,直线l与AD、BC两边分别相交于点E和点F.
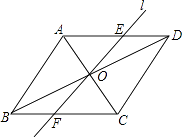
(1)求证:△AOE≌△COF;
(2)当α=30°时,求线段EF的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.

(1)求∠CDO的度数;
(2)求出点F坐标的表达式(用含t的代数式表示);
(3)当S△COD﹣S四边形COAF=7时,求抛物线解析式;
(4)当以B,C,O三点为顶点的三角形与△CEF相似时,请直接写出t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )

A.函数有最小值
B.对称轴是直线x=
C.当x< ,y随x的增大而减小
,y随x的增大而减小
D.当﹣1<x<2时,y>0 -
科目: 来源: 题型:
查看答案和解析>>【题目】直角三角形的外接圆半径为5cm,内切圆半径为1cm,则此三角形的周长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是cm.

相关试题

