【题目】如图,AB为⊙O的直径,AE为⊙O的切线,若tan∠ABE= ![]() ,AE=3,求BD的长.
,AE=3,求BD的长. 
参考答案:
【答案】解:∵AB为⊙O的直径, ∴∠ADB=90°,∴∠ADE=90°,
∵AE为⊙O的切线,
∴∠EAB=90°,
∵∠E=∠E,
∴△EAD∽△EBA,∴ ![]() ,
,
∴AE2=EDEB,
在Rt△AEB中,AE=3,tan∠ABE= ![]() ,
,
∴ ![]() ,∴AB=6,
,∴AB=6,
∴BE= ![]() =
= ![]()
∴32=ED3 ![]() ,
,
∴ED= ![]() ,
,
∴BD=BE﹣ED=3 ![]() ﹣
﹣ ![]() =
= ![]() .
.
【解析】由AB为⊙O的直径,得到∠ADB=90°,根据邻补角的定义得到∠ADE=90°,根据切线的性质得到∠EAB=90°,推出△EAD∽△EBA,根据相似三角形的性质得到 ![]() ,得到AE2=EDEB,根据三角函数的定义得到AB=6,由勾股定理得到BE=
,得到AE2=EDEB,根据三角函数的定义得到AB=6,由勾股定理得到BE= ![]() =
= ![]() ,即可得到结论.
,即可得到结论.
【考点精析】利用切线的性质定理对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示,BC∥AD,斜坡AB=40米,坡角∠BAD=60°,为防夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改造,经地质人员勘测,当坡角不超过45°时,可确保山体不滑坡,改造时保持坡脚A不动,从坡顶B沿BC削进到E处,问BE至少是多少米?(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 的图象与一次函数y=kx﹣3的图象在第一象限内相交于点A,且点A的横坐标为4.
的图象与一次函数y=kx﹣3的图象在第一象限内相交于点A,且点A的横坐标为4. 
(1)求点A的坐标及一次函数的解析式;
(2)若直线x=2与反比例函数和一次函数的图象分别交于点B、C,求线段BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装有分别标有汉字“幸”、“福”、“济”、“宁”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“福”的概率为多少?
(2)小颖从中任取一球,记下汉字后放回袋中,然后再从中任取一球,求小颖取出的两个球上汉字恰能组成“幸福”或“济宁”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠ABC=60°,对角线AC、BD相交于点O,将对角线AC所在的直线绕点O顺时针旋转角α(0°<α<90°)后得直线l,直线l与AD、BC两边分别相交于点E和点F.
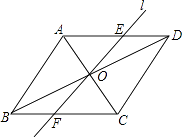
(1)求证:△AOE≌△COF;
(2)当α=30°时,求线段EF的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.

(1)求∠CDO的度数;
(2)求出点F坐标的表达式(用含t的代数式表示);
(3)当S△COD﹣S四边形COAF=7时,求抛物线解析式;
(4)当以B,C,O三点为顶点的三角形与△CEF相似时,请直接写出t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在研究相似问题时,甲、乙同学的观点如下: 甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )
A.两人都对
B.两人都不对
C.甲对,乙不对
D.甲不对,乙对
相关试题

