【题目】已知:如图,在△ABC中,∠A∶∠ABC∶∠ACB=3∶4∶5,BD,CE分别是边AC,AB上的高,BD,CE相交于H,求∠BHC的度数.

参考答案:
【答案】135°
【解析】
先设∠A=3x,∠ABC=4x,∠ACB=5x,再结合三角形内角和等于180°,可得关于x的一元一次方程,求出x,从而可分别求出∠A,∠ABC,∠ACB,在△ABD中,利用三角形内角和定理,可求∠ABD,再利用三角形外角性质,可求出∠BHC.
解:∵在△ABC中,∠A:∠ABC:∠ACB=3:4:5,
故设∠A=3x,∠ABC=4x,∠ACB=5x.
∵在△ABC中,∠A+∠ABC+∠ACB=180°,
∴3x+4x+5x=180°,
解得x=15°,
∴∠A=3x=45°.
∵BD,CE分别是边AC,AB上的高,
∴∠ADB=90°,∠BEC=90°,
∴在△ABD中,∠ABD=180°-∠ADB-∠A=180°-90°-45°=45°,
∴∠BHC=∠ABD+∠BEC=45°+90°=135°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为弘扬中华民族传统文化,某校举办了“古诗文大赛”,并为获奖同学购买签字笔和笔记本作为奖品.1支签字笔和2个笔记本共8.5元,2支签字笔和3个笔记本共13.5元.
(1)求签字笔和笔记本的单价分别是多少元?
(2)为了激发学生的学习热情,学校决定给每名获奖同学再购买一本文学类且定价为15元的图书.书店出台如下促销方案:购买图书总数超过50本可以享受8折优惠,学校如果多买12本,则可以享受优惠且所花钱数与原来相同,问学校获奖的同学有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某小区要用篱笆围成一矩形花坛,花坛的一边用足够长的墙,另外三边所用的篱笆之和恰好为
 米.
米.
(1)求矩形 的面积(用
的面积(用  表示,单位:平方米)与边
表示,单位:平方米)与边  (用
(用  表示,单位:米)之间的函数关系式(不要求写出自变量
表示,单位:米)之间的函数关系式(不要求写出自变量  的取值范围);怎样围,可使花坛面积最大?
的取值范围);怎样围,可使花坛面积最大?
(2)如何围,可使此矩形花坛面积是 平方米?
平方米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:EF∥AD,∠1=∠2,∠BAC=75°.将求∠AGD的过程填写完整.
 解:∵EF∥AD (已知)
解:∵EF∥AD (已知)∴∠2= ( )
又∵∠1=∠2 (已知)∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=75°(已知)
∴∠AGD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题有( )
①同旁内角互补;②互补的角是邻补角;③平方根、立方根是它本身的数是0和1;④
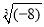 和﹣|﹣2|互为相反数;⑤4<
和﹣|﹣2|互为相反数;⑤4<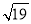 <5;⑥如果a∥b,a⊥c.那么b⊥c.
<5;⑥如果a∥b,a⊥c.那么b⊥c.A. 0个B. 1个C. 2个D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】永州市在进行“六城同创”的过程中,决定购买
 两种树对某路段进行绿化改造,若购买
两种树对某路段进行绿化改造,若购买 种树2棵,
种树2棵,  种树3棵,需要2700元;购买
种树3棵,需要2700元;购买 种树4棵,
种树4棵,  种树5棵,需要4800元.
种树5棵,需要4800元.(1)求购买
 两种树每棵各需多少元?
两种树每棵各需多少元?(2)考虑到绿化效果,购进A种树不能少于48棵,且用于购买这两种树的资金不低于52500元.若购进这两种树共100棵.问有哪几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 经过
经过  两点.
两点.
(1)求抛物线的解析式和顶点坐标;
(2)设点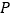 为抛物线上一点,若
为抛物线上一点,若  ,求点
,求点 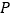 的坐标.
的坐标.
相关试题

