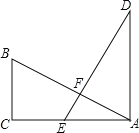
【题目】(本题7分)如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.
(1)判断线段AB与DE的数量关系和位置关系,并说明理由;
(2)连接BD、BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积证明勾股定理.
参考答案:
【答案】(1)AB=DE,AB⊥DE.理由见解析;(2)证明见解析.
【解析】试题分析:(1)根据垂直的定义可证得∠DAE=∠ACB=90°,然后根据ASA可证△ABC≌△DEA,从而得证AB=DE,且∠3=∠1,然后根据直角三角形的内角和等量代换可证得AB⊥DE;
(2)根据三角形的面积和四边形的面积,可知S四边形ADBE= S△ADE+ S△BDE,S四边形ADBE=S△ABE+S△ADB=![]() a2+
a2+![]() b2可得证符合勾股定理的逆定理.
b2可得证符合勾股定理的逆定理.
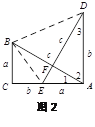
试题解析:(1)解:AB=DE, AB⊥DE.
如图2,∵AD⊥CA,∴∠DAE=∠ACB=90°,
∵AE=BC,∠DAE=∠ACB,AD=AC,∴△ABC≌△DEA,∴AB=DE,
∠3=∠1,∵∠DAE=90°,∴∠1+∠2=90°,∴∠3+∠2=90°,
∴∠AFE=90°,∴AB⊥DE.
(2)如图2,∵S四边形ADBE= S△ADE+ S△BDE=![]() DE·AF+
DE·AF+![]() DE·BF=
DE·BF=![]() DE·AB =
DE·AB =![]() c2,
c2,
S四边形ADBE=S△ABE+S△ADB=![]() a2+
a2+![]() b2,
b2,
∴![]() a2+
a2+![]() b2=
b2=![]() c2,∴a2+b2=c2.
c2,∴a2+b2=c2.
-
科目: 来源: 题型:
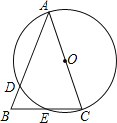
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小慧去花店购买鲜花,若买6支玫瑰和4支百合,则她所带的钱还剩下8元:若买4支玫瑰和6支百合,则她所带的钱还缺2元.若只买10支玫瑰,则她所带的钱还剩下( )
A.32元B.30元C.28元D.24元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.
(1)求证:直线BC是⊙O的切线;
(2)若OA=3,AB=2,求BP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知月球表面的最高温度是127°C,最低温度是-183°,则月球表面的温差是( )
A. 56°C B. 65° C. 300°C D. 310°C
-
科目: 来源: 题型:
查看答案和解析>>【题目】汛期的某一天,某水库上午8时的水位是45m随后水位以每小时0.6m的速度上涨,中午12时开始开闸泄洪,之后水位以每小时0.3m的速度下降,则当天下午6时,该水库的水位是( )
A. 45.4m B. 45.6m C. 45.8m D. 46m
-
科目: 来源: 题型:
查看答案和解析>>【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
(1)请你补全这个输水管道的圆形截面;
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.

相关试题

