【题目】下列命题正确的是( )
A.一组对边相等,另一组对边平行的四边形一定是平行四边形
B.对角线相等的四边形一定是矩形
C.两条对角线互相垂直的四边形一定是菱形
D.两条对角线相等且互相垂直平分的四边形一定是正方形
参考答案:
【答案】D
【解析】
试题分析:A、一组对边相等,另一组对边平行的四边形不一定为平行四边形,例如等腰梯形满足一组对边相等,另一组对边平行,但不是平行四边形;
B、对角线相等的四边形不一定为矩形,例题等腰梯形的对角线相等,但不是矩形,应改为对角线相等的平行四边形为矩形;
C、对角线互相垂直的四边形不一定为菱形,例如:画出图形,如图所示,AC与BD垂直,但是显然ABCD不是菱形,应改为对角线互相垂直的平行四边形是菱形;
D、两条对角线相等且互相垂直平分的四边形是正方形,根据题意画出相应的图形,如图所示,根据对角线互相平分,得到四边形为平行四边形,再由平行四边形的对角线相等,得到平行四边形为矩形,最后根据矩形的对角线互相垂直得到矩形为正方形.
解:A、一组对边相等,另一组对边平行的四边形不一定是平行四边形,
例如等腰梯形,一组对边平行,另一组对边相等,不是平行四边形,
故本选项为假命题;
B、对角线相等的四边形不一定是矩形,
例如等腰梯形对角线相等,但不是矩形,
故本选项为假命题;
C、两条对角线互相垂直的四边形不一定是菱形,
如图所示:AC⊥BD,但四边形ABCD不是菱形,本选项为假命题;

D、两条对角线相等且互相垂直平分的四边形是正方形,

已知:四边形ABCD,AC=BD,AC⊥BD,OA=OC,OB=OD,
求证:四边形ABCD为正方形,
证明:∵OA=OC,OB=OD,
∴四边形为平行四边形,又AC=BD,
∴四边形ABCD为矩形,
∵AC⊥BD,
∴四边形ABCD为正方形,则本选项为真命题,
故选D
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:4ab-a2-[2(a2+ab)-3(a2-b2)],其中a=-1,b=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正数的x的平方根是2a﹣3与5﹣a,求a和x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD,AB=
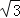 ,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.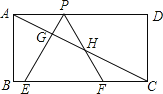
(1)求△PEF的边长;
(2)在不添加辅助线的情况下,当F与C不重合时,从图中找出一对相似三角形,并说明理由;
(3)求证:PH﹣BE=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三角形的内部,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形( )
A. 三条中线的交点
B. 三条角平分线的交点
C. 三条边的垂直平分线的交点
D. 三条高的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的一边长为a+b,另一边长比这条边长b,第三边长比这条边短a-b(0<b<a).
(1)求这个三角形的周长(用含a、b的代数式表示);
(2)若a=5,b=3,求三角形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程a+x=5-(2a+1)x的解也是方程-x=x+2的解,则a的值是( )
A. -5 B. -6 C. -7 D. -8
相关试题

