【题目】如图,已知△ABC中,∠B=∠C,AB=AC=10cm,BC=8cm,点D为AB的中点.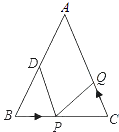
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC边上相遇?
参考答案:
【答案】
(1)解:①∵t=1s,
∴BP=CQ=3×1=3cm,
∵AB=10cm,点D为AB的中点,
∴BD=5cm.
又∵PC=BC﹣BP,BC=8cm,
∴PC=8﹣3=5cm,
∴PC=BD.
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中, 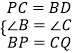 ,
,
∴△BPD≌△CQP(SAS).
②∵vP≠vQ ,
∴BP≠CQ,
若△BPD≌△CPQ,∠B=∠C,
则BP=PC=4cm,CQ=BD=5cm,
∴点P,点Q运动的时间 ![]() ,
,
∴ ![]() cm/s
cm/s
(2)解:设经过x秒后点P与点Q第一次相遇,
由题意,得 ![]() x=3x+2×10,
x=3x+2×10,
解得 ![]() .
.
∴点P共运动了 ![]() ×3=80cm.
×3=80cm.
△ABC周长为:10+10+8=28cm,
若是运动了三圈即为:28×3=84cm,
∵84﹣80=4cm<AB的长度,
∴点P、点Q在AB边上相遇,
∴经过 ![]() s点P与点Q第一次在边AB上相遇
s点P与点Q第一次在边AB上相遇
【解析】(1)①根据时间和速度分别求得BP、BD、PC、QC的长,根据SAS判定两个三角形全等.②根据全等三角形对应边相等可得到BP=PC=4cm,CQ=BD=5cm,再根据路程=速度×时间公式,先求得点P运动的时间,再求得点Q的运动速度;(2)由于点Q的速度快,且在点P的前边,所以要想第一次相遇,则应该比点P多走等腰三角形的两个腰长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y1=x和直线l2:y2=﹣2x+6相交于点A,直线l2与x轴交于点B,动点P沿路线O→A→B运动.
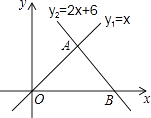
(1)求点A的坐标,并回答当x取何值时y1>y2?
(2)求△AOB的面积;
(3)当△POB的面积是△AOB的面积的一半时,求出这时点P的坐标. -
科目: 来源: 题型:
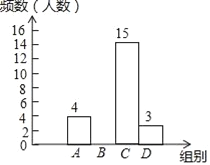
查看答案和解析>>【题目】为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
组别
成绩x(分)
频数(人数)
A
8.0≤x<8.5
a
B
8.5≤x<9.0
8
C
9.0≤x<9.5
15
D
9.5≤x<10
3
(1)图中a= ,这次比赛成绩的众数落在 组;
(2)请补全频数分布直方图;
(3)学校决定选派本次比赛成绩最好的3人参加全市中学生朗诵比赛,并为参赛选手准备了2件白色、1件蓝色上衣和黑色、蓝色、白色的裤子各1条,小军先选,他从中随机选取一件上衣和一条裤子搭配成一套衣服,请用画树状图法或列表法求出上衣和裤子搭配成不同颜色的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b=3,ab=﹣2,则a2+b2的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是( )
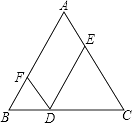
A.5
B.10
C.15
D.20 -
科目: 来源: 题型:
查看答案和解析>>【题目】整式A与m2+2mn+n2的和是(m﹣n)2 , 则A= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径AB=4,∠BAC=30°,AC交⊙O于D,D是AC的中点.
(1)过点D作DE⊥BC,垂足为E,求证:直线DE是⊙O的切线;
(2)求
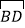 与线段DE、BE围成的阴影面积.
与线段DE、BE围成的阴影面积.
相关试题

